尝试理解神经网络的工作原理!旧文新发。
分类问题引入
少维度分类
如下图是一个北京和长治的房价对比图:
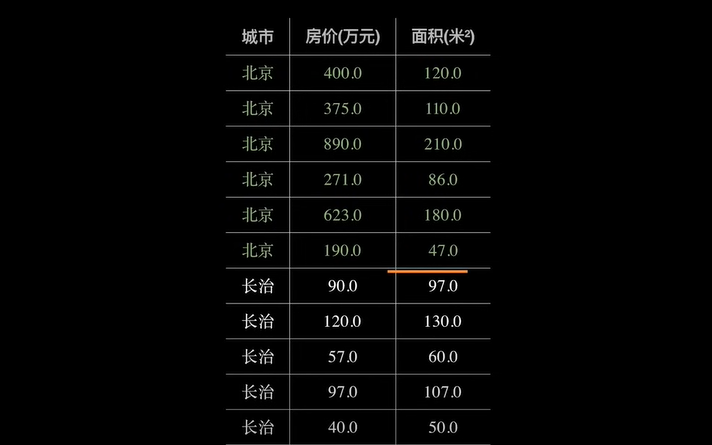
如上使用表格的形式表示,可能不是很直观。换成如下的坐标系就能很清楚的看出来区别:
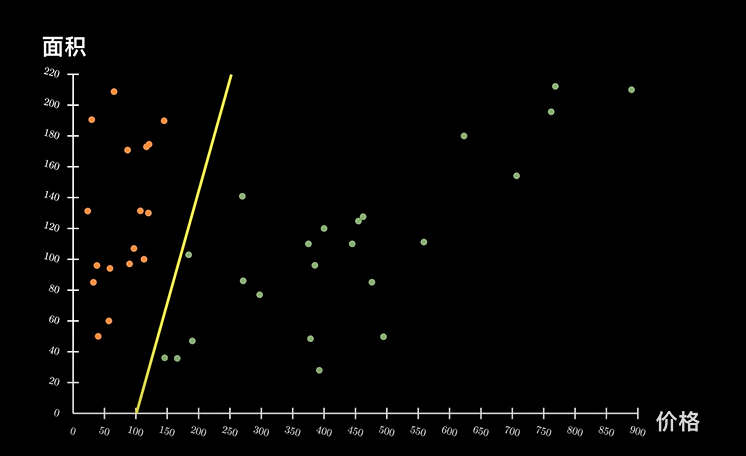
图中标注一条黄色的数据线,可以看出,黄线左边的属于北京,右边的属于长治。
我们可以将问题进一步分析,使其变得更简单:在日常生活中,根据我们的经验知道,决定房子价格的因素其实是
价格/面积 = 平方价
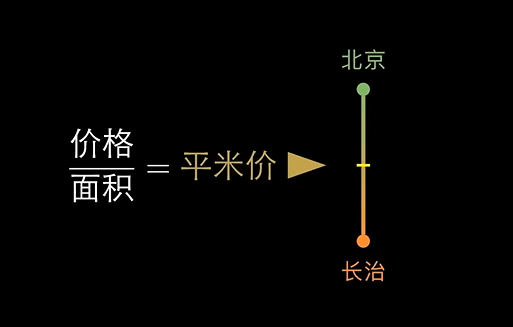
高者属于北京,低的则是长治。为此,我们可以找到一个阈值,将其进行划分。
上述就是最简单的分类问题,只有价格和面积两个维度。
多维度分类
在现实生活中,判断房子值不值得购买。不可能只有 房价 & 面积 两个因素,可能还有 楼层、通勤、年限、环境 等其他因素。问题的本质还是一样的,最终我们都是根据对这些数据进行分析,判断值不值得购买。

这个阈值怎么寻找,用什么样的方式去判定。或者说这个函数是什么样子?
推导数学结论
这里,我们设 房价 = x,面积 = y:
设 房价 为 x,面积 为 y。
则有
x / y = 平米价
设将北京和长治区分开的阈值为 0.69 ,则 x/y > 0.69 就是北京,反之则是长治。
接下来我们将公式变形,即可得到函数 f 的函数表达式
f(x,y) = x - 0.69y = 0
从公式我们可以看出,这时候的阈值变成了 0,大于 0 表示北京,小于表示长治。这里只考虑了房价和面积两个因素。更现实的情况是:因为其他因素的参与,阈值可能不会恰好等于 0,可能是 101。这里我们就可以加入一个偏移量 对阈值进行校准。
f(x,y) = x - 0.69y - 101 = 0
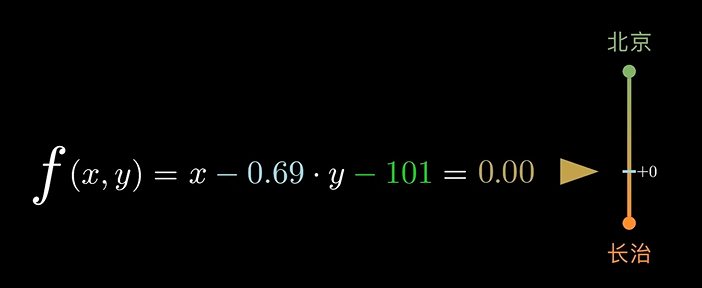
此时,我们观察这个函数表达式:
如果 y 的取值增加了 100,函数值势必发生变化。但是只要同时对 x 的值做出修正,就可以抵消函数值发生的变化,即
f(x,y) = x - 0.69y - 101 = 0
[+69] \quad [+100]
此时,在函数 f 中,x 的 +69 和 y 的 -100 在数学关系上等价。但是在物理意义上,x 代表的是房价,y 代表的是面积。单位/量纲 不同,无法进行公度。
f(x,y) = x - 0.69y - 101 = 0
[+69] \quad [+100]
(万元) \quad (米^2)
在当前的函数中,他们是可以进行换算的,因为他们都对函数 f 的取值做出了贡献。换算的方式来自于对函数值贡献的大小。即:
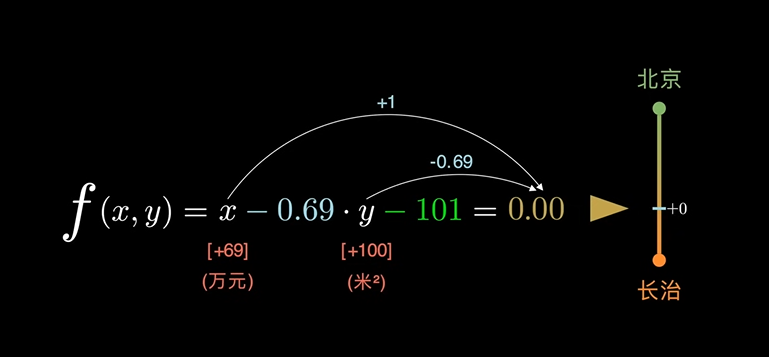
从中可以看出,x 和 y 对函数值的贡献正好是 x 和 y 的系数。
回头看将才数据维度很多的情况:
设 数据维度依次为 x_1, x_2, x_3.....
则
f(x_1, x_2, x_3, x_4...) = x_1 + x_2 + x_3 + x_4 + b
根据上述对 x 和 y 的推导,我们可以将其变成:
w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + ... + b = y
其中函数值 y 就是房子是否值得购买的依据。
根据上面我们的推导,这样的函数是有意义的:
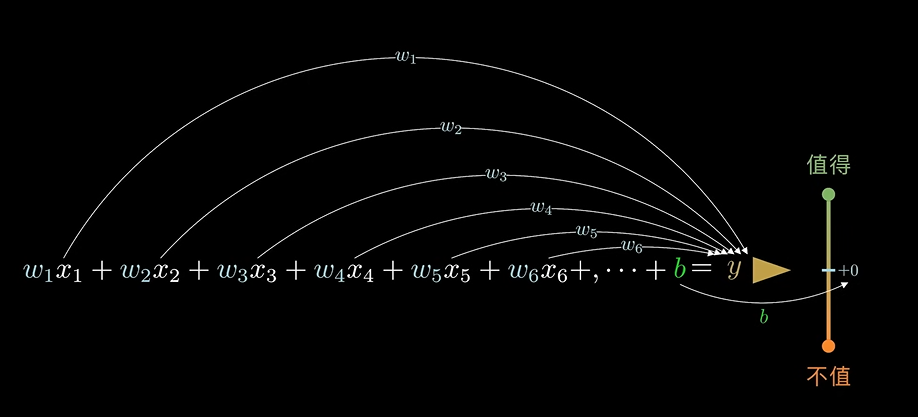
w 的系数为对函数值的贡献程序,b 为阈值的偏移量。
规范数学表达为:w -> 权重系数、b -> 偏置系数。
在坐标系中表达为:(为了画图方便,回到二维系数表达)
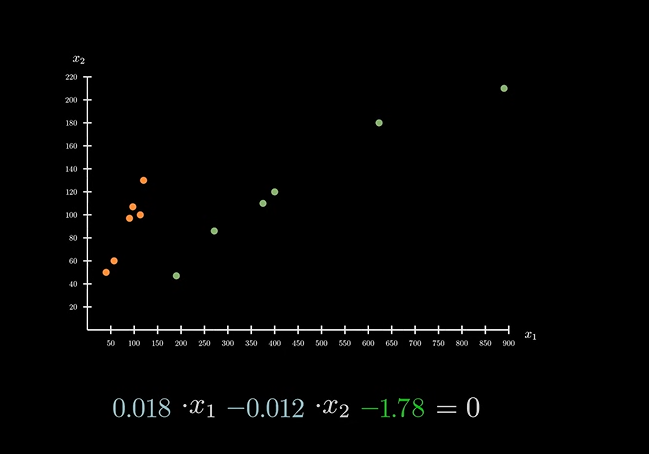
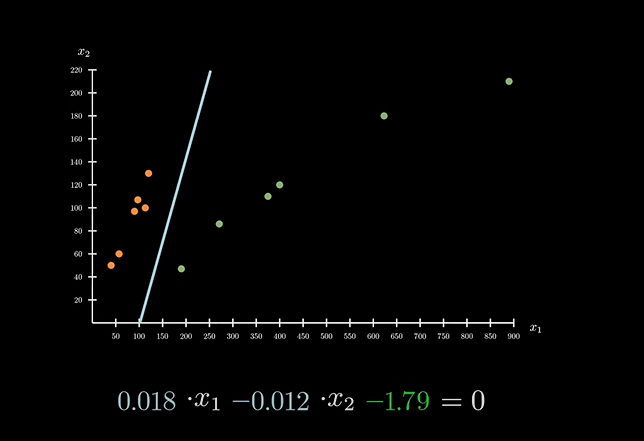
前面讨论的阈值即为下图中的分界线:
加入参数升维
根据数学原理,不同的阈值即代表了不同的分界线。当这条直接确定下来之后,对数据的划分也随之确定。将不同的系数带入变量 x 和 y 就可以得到不同的结果。
如果我们引入更多的维度系数,对坐标系升维。则:
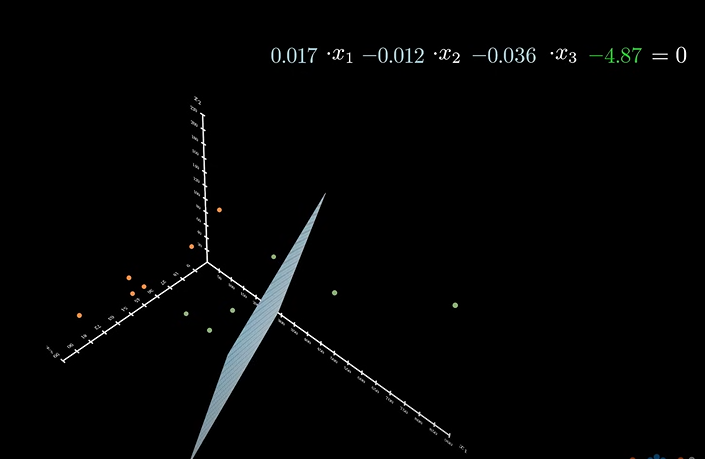
在更高维度中,经常使用向量和矩阵的表达形式:
w_1x_1 + w_2x_2 + w_3x_3 + w_4x_4 + \cdots + b \\ \\
将其转化为向量和矩阵的表达式为:\\\\
\left[
\begin{matrix}
w_1 & w_2 & w_3 & w_4 & \cdots
\end{matrix}
\right]
·
\left[
\begin{matrix}
x_1 \\ x_2 \\ x_3 \\ s_4 \\ \cdots
\end{matrix}
\right]
+b \\\\
代表行向量和列向量逐项相乘,再相加 \\
为了让表达形式更加紧凑,通常对行向量进行转置,再进行点积运算:\\\\
\left[
\begin{matrix}
w_1 \\ w_2 \\ w_3 \\ w_4 \\ \cdots
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
x_1 \\ x_2 \\ x_3 \\ s_4 \\ \cdots
\end{matrix}
\right]
+b \\\\
通常向量和矩阵,通常使用大写字母来表示,即:\\\\
f(X) = W^\mathrm T · X + b \\
另外一种表达形式是将偏置系数同样写进到矩阵中: \\\\
\left[
\begin{matrix}
w_1 \\ w_2 \\ w_3 \\ w_4 \\ \cdots \\ b
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
x_1 \\ x_2 \\ x_3 \\ s_4 \\ \cdots \\ 1
\end{matrix}
\right] \\\\
函数表达式为:\\
f(X) = W^\mathrm T · X
在前面的讨论中,确定了数据的阈值(分界线之后)。下一步行为在 机器学习 中称为 决策/预测。对于一个新输入的数据,通过 x 和 y 在坐标系中的位置来判断处于分界线哪一边。在程序中,并不能直接去看图像。而是要将参数值代入到函数中,计算出函数值,和 0 比较,进行判断。
到这一步,机器学习的问题变得相对简单,而机器学习的难点是在于如何确定一条最好的分界线,即确定阈值。这个过程叫做训练/学习。和动规,贪心等算法不同的是,**机器学习只需要在刚开始时对大量复杂的数据进行计算,确定出来关系。在面对新数据时,只需要进行简单的运算就可以达成目标。**那么,机器学习并没有减少算法的复杂度,相比之下而言,只是提高的 决策/训练 的应用效能。
所以接下来,我们将了解如何去
训练和学习。
训练 & 学习
训练/学习 的目的很明确,即在坐标系中确定这条分界线!同样,机器学习的难点也在这里。
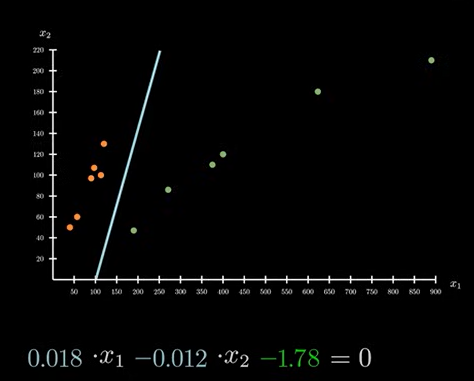
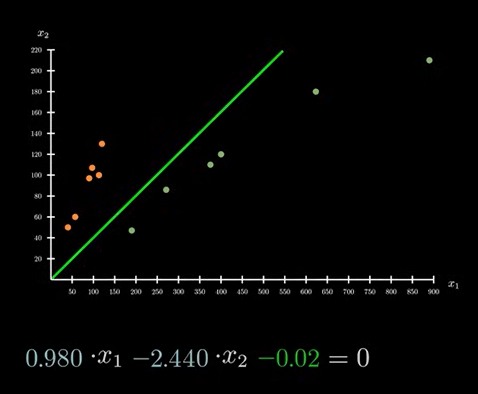
如图,上述两条直线,都能对现有数据进行完美划分。但是哪条直线是最优解?往往现实情况并不是这样,而是下图所示:
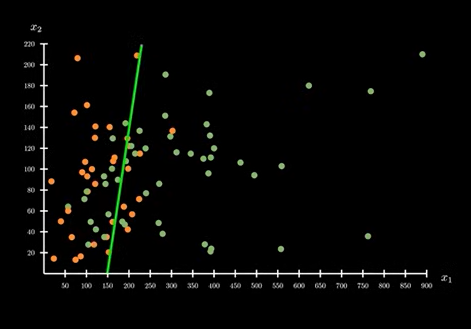
即不存在这样的最优解,可以将数据进行完美划分。只能从现有的直线中,挑选一条符合大多数情况,能将大多数数据区分开的直线。
那么如何确定这条直线是不是符合现有的预期?对此,**就需要有一个判断分界线好坏的判断标准。**在面对不同的数据集时,挑选出的直线可能不同,如上图所示。随着越来越多的数据,直线也会随之变化。注意:机器学习的目的是预测,而不是训练。在当前的数据集范围中,只能做到当前情况分界线最好,并不能保证对新来的数据也是最好。这也是选择判断标准最困难的地方。当我们选择了一个判断标准之后,标准之中就包含了我们对未来数据的一种预测。这个预测无法在数学逻辑上找到答案,所以要想解决这个问题,就必须要引入额外的公设。
引入额外公设
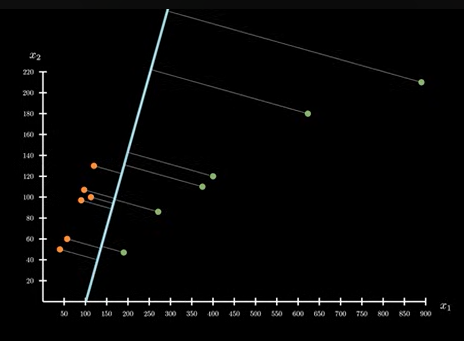
从图中看,每个点到分界线的距离大小不一,所有这些点中,对分界线最小的哪一个,我们可以把它看作是分界线对数据划分的间隔:
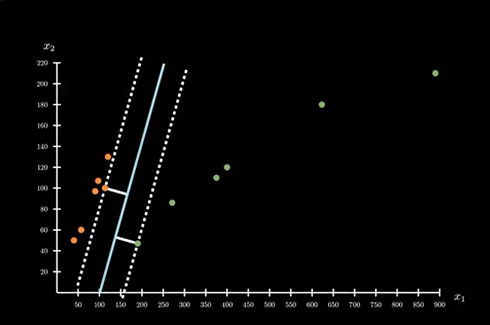
通过已有的直觉判断,应该是分界线到点的距离越大越好。其中的间隔可以容纳更多的点。
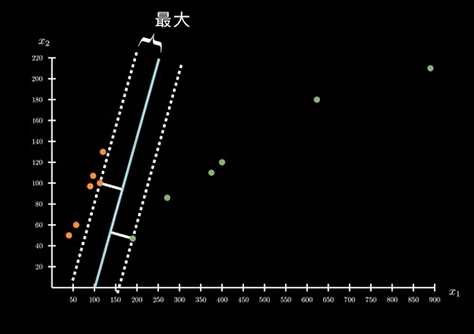
公设条件 1
因此,我们可以提出这样一个公设:间隔越大越好
那么,这里的间隔如何计算,我们需要将其交给计算机去判断,所以我们需要找到间隔计算的表达式:
-
我们需要知道点到直线的距离 ,表达式为(带入 x 和 y 无法直接得到点到直线的距离,需要做一些修饰):
\frac{1}{\|W\|_2} \|f(X)\| \\
\|W\|_2 \text{(权重系数的 } L_2 \text{ 范数)这里的 } L_2 \text{ 范数可以理解为 勾股定理在更高维度上的扩展,即} \\
\|W\|_2 = \sqrt{w_1^2 + w_2^2 + w_3^2 + w_4^2 + \cdots} \\
\text{对向量里的每个分量进行平方再开方。} -
对上述的每个点进行 1 的运算,即可得到所有点到直线的间隔(用 M(W) 来表示直线间隔函数):
M(W)=\underset {i=1,2,3 \cdots N}{min}\frac{1}{\begin{Vmatrix}W\end{Vmatrix}}_2\begin{vmatrix}f(X^{(i)})\end{vmatrix} \\\\ -
将所有数据带入上述公式,在不考虑机器算力的情况下,计算机就可以完成这些计算。
进行上述操作之后,我们就能得到的结果。这一切的前提是我们对 f(x) 这样的函数值进行了上述修饰。既然这里是公设,那么它就不唯一。这里还可以有第二种公设。同样,我们能偶利用的只有函数值,仍然对其进行修饰,得出前提假设。
这次的修饰是对其进行 sigmoid(f(x)) 操作:
sigmod(f(x)) \in (0,1)
通过 sigmoid 操作,可以将函数值缩放到 0 ~ 1 之间。sigmoid函数图像如下:
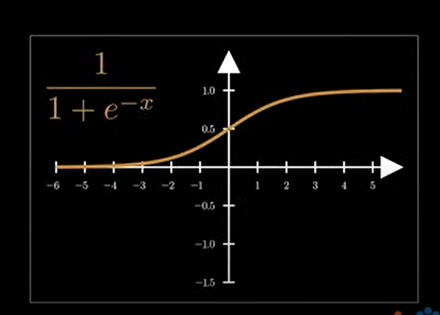
定义域为全体实数,值域为 0 - 1 的开区间。0 - 1 的开区间,很容易让我们想到概率,那么我们是否可以把经过修饰后的函数值看作是一个概率值呢?
公设条件 2
我们将函数值看作是如下的条件概率:
P(X = X^{(i)} \mid W)=sigmod(f(x^{(i)}))
这个概率的意义就代表了某一个数据在北京还是长治的可能性。
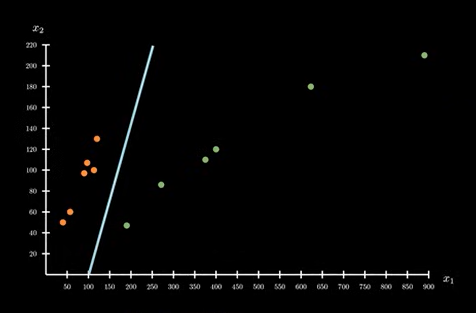
在当前的数据情况下,北京的函数值大于 0 ,长治的函数值小于 0 。
北京:P(X = X^{(i)} \mid W)=sigmod(f(x^{(i)})) \\\\
长治:P(X = X^{(i)} \mid W)=sigmod(-f(x^{(i)})) \\ 长治的函数值小于 0 ,所以要对函数值取附属再进行 sigmoid 操作。 \\\\
概率值越大就表明属于 “北京/长治” 的可能性越大,反之则越小。
基于当前的理解,我们就可以提出新的公设条件(第二种公设):
概率(似然)值最大最好
概率值最大,就应该是所有点的概念都最大,他们是相乘的关系。即我们需要找的就是当
\underset{W} {max} \prod_{i=0}^N P(X = X^{i}\mid {W})· \prod_{j = 0}^M P(X = X^{(i)} \mid {W})
表达式取值最大时,系数 W 的值。上述表达式最常见的形式是:使用 log 运算符将连乘变为连加。
第三种公设:现在我们可以假想出一个如下的函数 T(X) ,它可以对数据进行完美分类。
T(X)=
\begin{cases}
1: X \in {北京} \\
0: X \in {长治}
\end{cases}
任何一个数据的输入,都可以完美的判断出它属于北京还是长治。北京的函数值为 1 ,长治的函数值为 0 。图像表示为:
公设条件 3
那么,我们知道,在现实情况中,这种函数一定不存在,总是会有各种各样的误差和噪声对 T(X) 函数产生影响。这里我们用 ϵ 表示给函数叠加了一个噪声。它不再变得完美了。函数的输出值依然是会接近 0 和 1。
T(X)+\epsilon=
\begin{cases}
1+\epsilon: X \in {北京} \\
0+\epsilon: X \in {长治}
\end{cases}
这个时候 sigmoid 函数就可以派上用场了,我们就可以用它来表示受到噪声干扰后的 T(X) 函数。
T(X)+\epsilon=sigmoid(f(X))
图象如下所示:
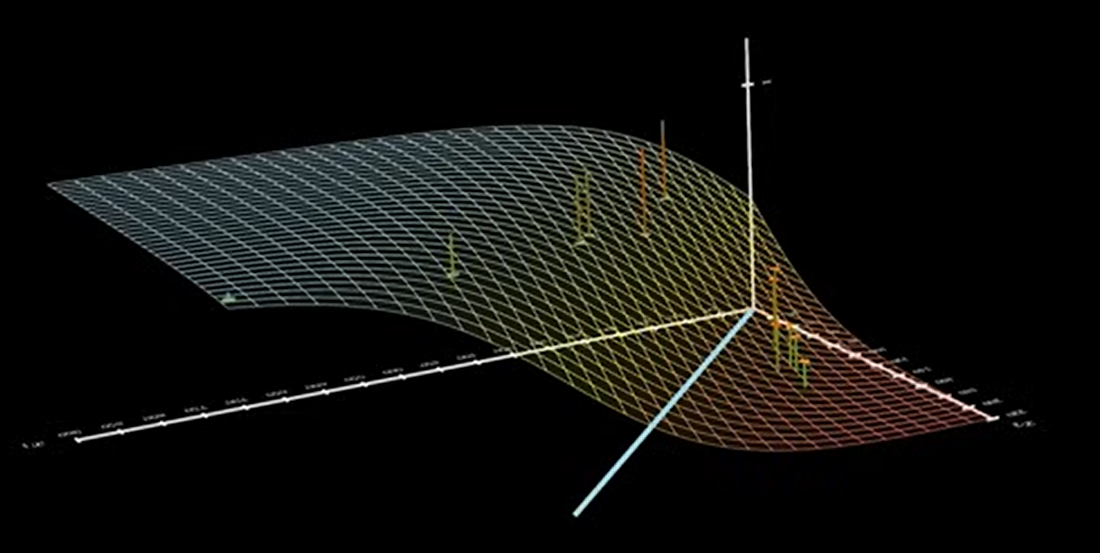
这个时候每一个数据得到的 sigmoid 函数值与他们再 T 函数中取值的偏差就是叠加之后的噪声 ϵ 。最好的分界线,必然是 ϵ 最小的时候对应的分界线。即:方差最小最好。
\underset{W}{min}\sum_{i=0}^N(y-\hat{y})^2
y=
\begin{cases}
1: X \in {北京} \\
0: X \in {长治}
\end{cases}
\hat{y}=sigmoid(f(X))
第三种公设的表达式为:
\sigma^2=(y-\hat{y})^2
上述提到的三种公设表示为:
- 粉红色:方差最小最好;
- 橙色:概率最大最好;
- 绿色:间隔最大最好。
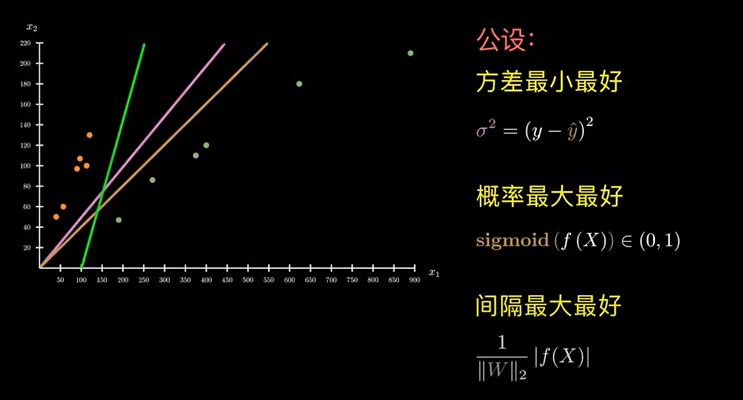
我们知道,公设不同,得到的结果也不同,到底那种结果最好?
没有理论上的标准答案,还是要看真实问题是什么。
这里的三种公设条件可以表示为:
公设:\begin{cases}
修饰公度结果 \\
为公度结果赋予现实意义 \\
用现实意义将一直外推至未知
\end{cases}
所有的公设得到的结果都是对已知现实的总结归纳,是对未知情况的经验总结。
虽然这里写出了判断标准的数学方程,但是求出解析解几乎不可能,困难重重。这里如何选择最合适的算法更快、更好的求出函数表达式的数值解。就是机器学习的另一项重要工作:算法。
虽然算法非常多,但是针对神经网络,提到算法就是在特指 梯度下降法。
公设的常见叫法是策略。 算法,策略加上模型,就是机器学习的三大要素。
机器学习中的模型
数据模型分类问题
接下来我们要看的就是模型。模型简单来说就是对数据的分类,为什么要选择直线?如下的数据分类图:
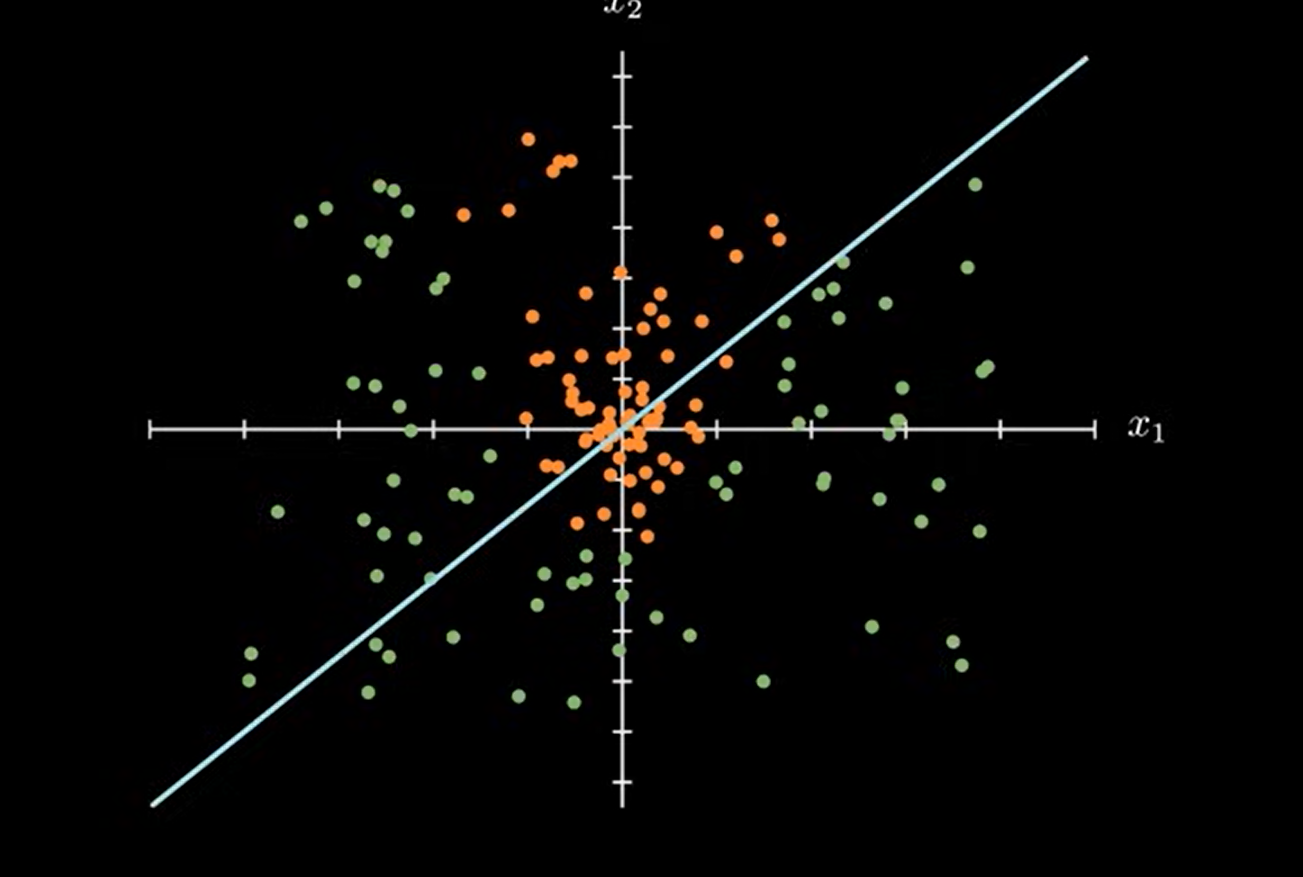
面对这种数据分类的时候,无论直线怎么放置,都会存在问题。但是使用下面的抛物线,就能准确划分数据。
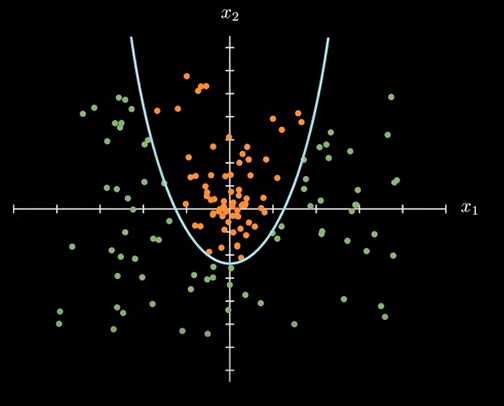
抛物线方程如下:可以看到相比直线方程,只多了一个 x1 系数的二次项
w_1x_1^2+w_2x_1-x_2+b=0
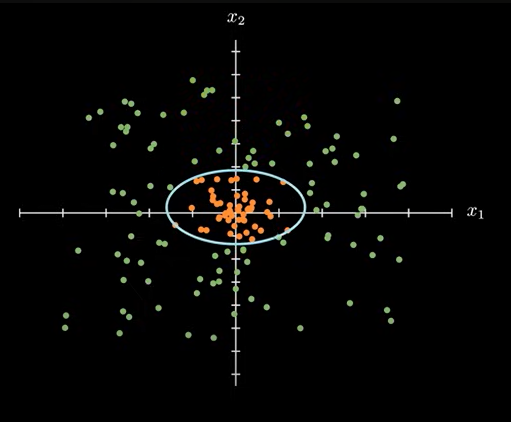
这里,如果我们再增加 一个 x2 维度的二次项,还可以变化成为椭圆形的分界线。
w_1x_1^2+w_2x_2^2+w_3x_1+w_4x_2+b=0
增加 x3 系数的二次项时,会变成双曲线。对数据分类更加准确。
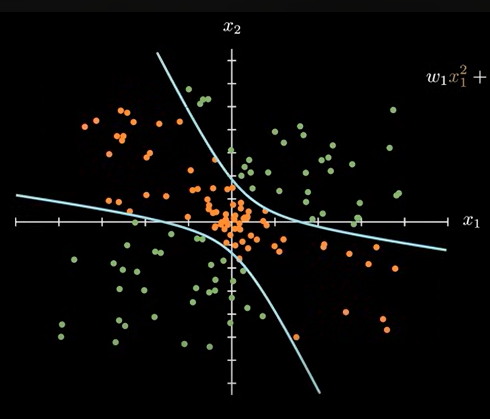
w_1x_1^2+w_2x_22+w_3x_1x_2+w_4x_1+w_5x_2+b=0
前人已经证明过,只要增加更多的高次项,那么不论多么奇怪的分割线都可以表示出来。
随着项数的增加,复杂程度会越来越大。也就是说模型的复杂程度越高。
为了图形表示方便,暂时这里只针对 x1 维度增加更高次项。
\cdots+w_1x_1^3+w_2x_1^2+w_3x_1+w_4x_2+b=0
图像表示为:
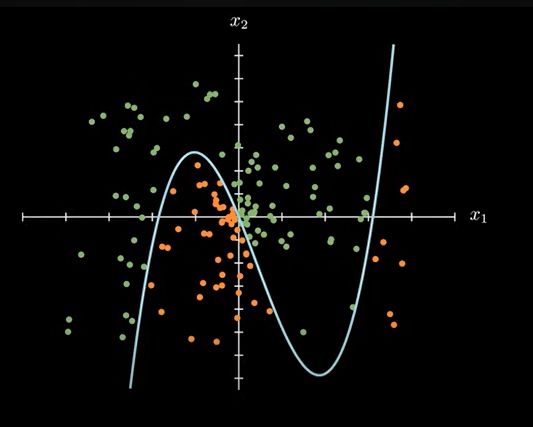
用向量点积的形式表示为:
\left[
\begin{matrix}
\cdots \\ 0.00 \\ 0.00 \\ -0.20 \\ 0.50 \\ 4.60 \\ -1.00
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
\cdots \\ x_1^5 \\ x_1^4 \\ x_1^3 \\ x_1^2 \\ x_1 \\ x_2
\end{matrix}
\right] \\\\
分类 & 回归问题
机器学习里讨论的模型复杂程度其实就是曲线的复杂程度。虽然我们这里讨论的是分类问题,其实和回归问题在模型上并没有本质的区别。比如上述的曲线,可以是对数据的分类,也可以看作是对这些数据的拟合。
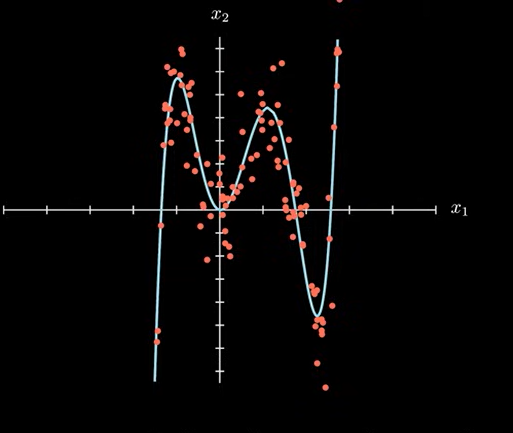
下面我们还是讨论分类问题。
引入神经网络
既然直线模型的局限性这么大,我们是不是可以提高模型的复杂程度呢?我们这次讨论的重点——神经网络就是一种提高模型负责程度的方法。
下图就表示一个神经网络:
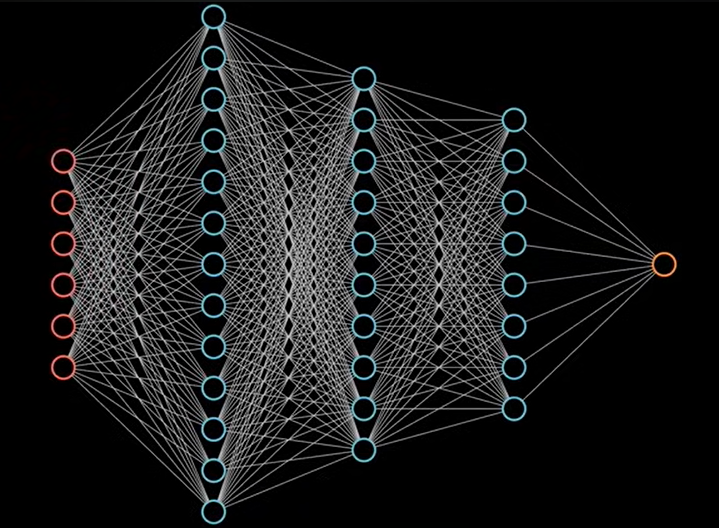
红色表示输入层,输入层的输出输入到神经网络,其中每一个神经元都和上一层,下一层互相连接。称为全连接神经网络。这里,我们单独拿出一个最简单的结构:
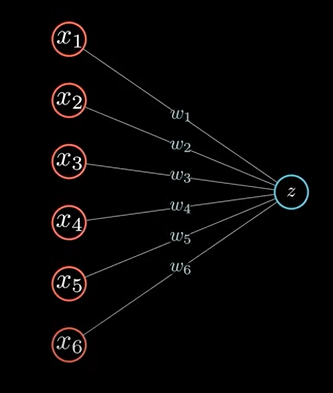
这里的每一条代表的是对应的权重系数。这个结构,其实就表示为一个线性方程,表达式如下:
w_1x_1+w_2x_2+w_3x_3+w_4x_4+w_5x_5+w_6x_6+b=z
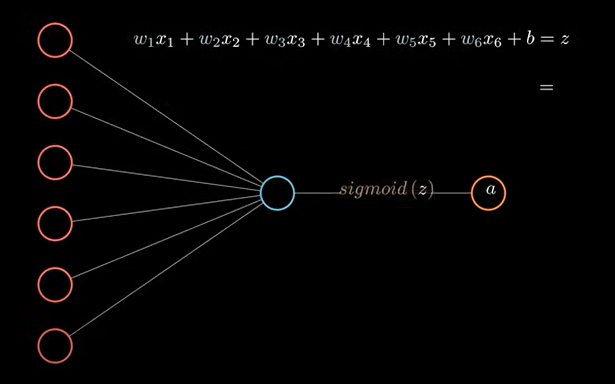
经过 sigmoid(f(x)) 激活函数计算输出结果到下一层。
激活函数
神经网络对激活函数的选择是有要求的,sigmoid 只是符合要求的函数之一。这个激活的过程不会在神经网络中表示出来,只是在神经元中显示。

因为后面需要使用坐标系来展示,所以这里只讨论二维情况:
其用向量表示为:
\left[
\begin{matrix}
x_1\\x_2
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_1\\w_2
\end{matrix}
\right]
+[b]
= [z]\\
sigmoid(z)=a
\\\\
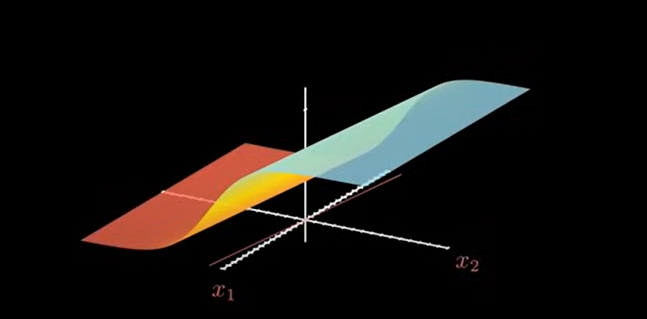
表达式的输入输出在坐标系中显示为如下图的一个曲面:对应的分界线就是 x1 和 x2 平面上的红色直线。
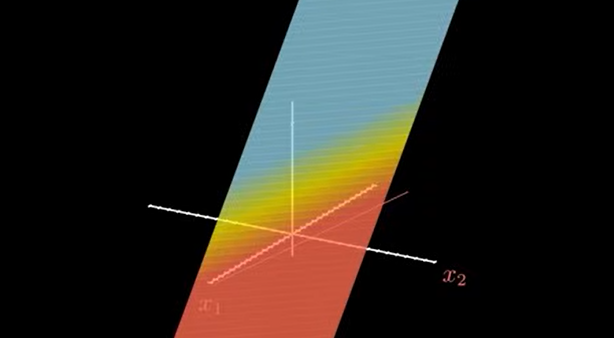
如果不存在激活函数,就只是一个面,如图:
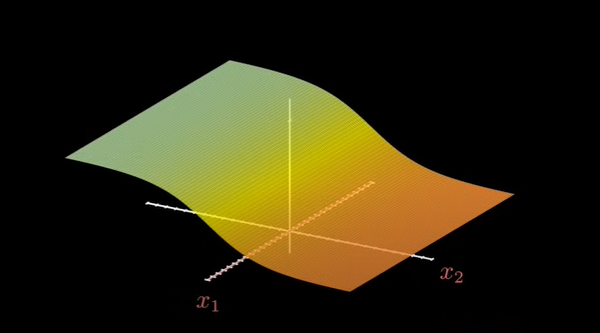
再加入一个神经元时,表示如下:
\left[
\begin{matrix}
x_1^{[0]}\\x_2^{[0]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_1^{[1]}\\w_2^{[1]}
\end{matrix}
\right]
+[b^{[1]}]
= [z^{[1]}]\\\\
sigmoid(z^{[1]}=a^{[1]}
\\\\
这里用中括号中的上标数字表示是神经元的第几层。
输入层对应的是 0 层。第一层的输出结果会作为第二层的输入。
[a^{1}]^\mathrm T·[w_1^{[2]}]+[b^{[2]}]=[z^{[2]}] \\
sigmoid(z^{[2]}) = a^{[2]}
增加一层神经元之后,图像并不会有多大的变化,仍然是下面这种曲面:
接下来就会发生变化,我们在多加一个神经元之后,
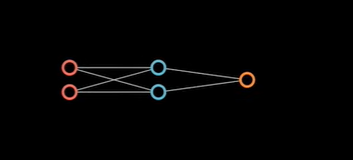
每个神经元都有 W1, W2 和 b 一组系数。这时候 W 就不再是向量,而是矩阵。不过仍然是进行线性运算。
\left[
\begin{matrix}
x_1^{[0]}\\x_2^{[0]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_{1.1}^{[1]} \quad w_{2.1}^{[1]} \\w_{1.2}^{[1]} \quad w_{2.2}^{[1]}
\end{matrix}
\right]
+[b_1^{[1]} \quad b_2^{[1]}]
= [ \quad z_2^{[1]}]\\\\
转置之后:\\\\
\left[
\begin{matrix}
x_1^{[0]}\\x_2^{[0]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_{1.1}^{[1]} \quad w_{2.1}^{[1]} \\w_{1.2}^{[1]} \quad w_{2.2}^{[1]}
\end{matrix}
\right]
+
\left[
\begin{matrix}
[b_1^{[1]} \\ b_2^{[1]}
\end{matrix}
\right]^\mathrm T
=
\left[
\begin{matrix}
[z_1^{[1]}] \\ z_2^{[1]}
\end{matrix}
\right]^\mathrm T \\\\
激活函数也变成使用向量表示的形式:
sigmoid(Z^{[1]}) = A^{[1]}
\\
这里表示每一项,每一个分量都要经过
sigmoid计算。
第二层的输入也会相应变成两个:
\left[
\begin{matrix}
a_1^{[1]}\\
a_2^{[1]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_1^{[2]} \\
w_2^{[2]}
\end{matrix}
\right]
+
\left[
\begin{matrix}
b^{[2]}
\end{matrix}
\right]
=
\left[
\begin{matrix}
z^{[2]}
\end{matrix}
\right] \\\\
sigmoid(Z^{[2]}) = a^{[2]}
此时的图像会变的更加多样:
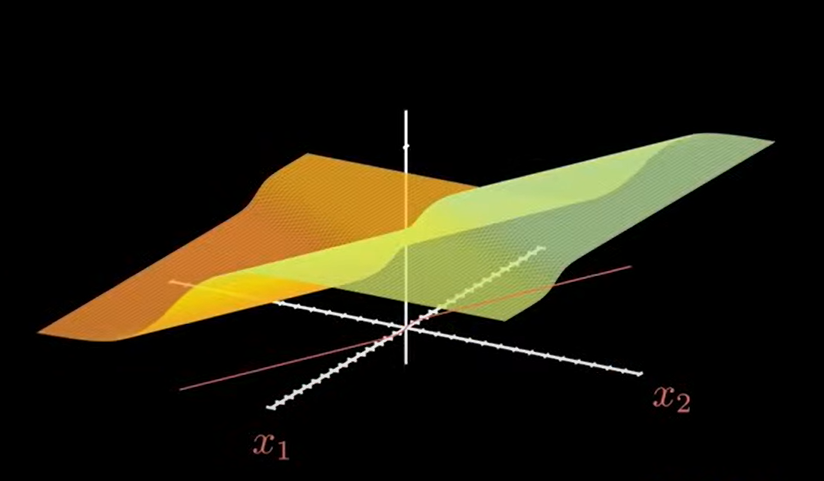
尤其是分界线,已经不止是一条直线了,而是发生了弯曲。
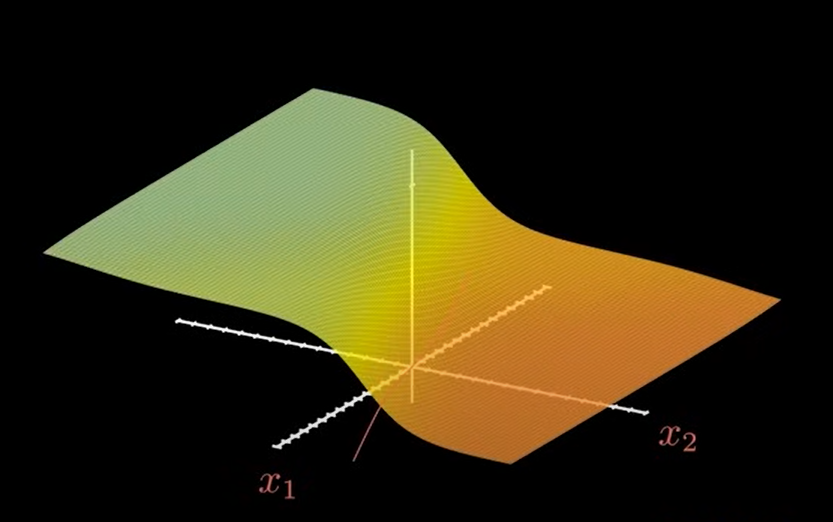
如果我们继续增加神经元,增加到四个:
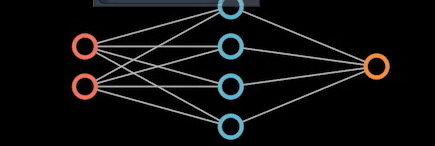
\left[
\begin{matrix}
x_1^{[0]}\\x_2^{[0]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_{1.1}^{[1]} \quad w_{2.1}^{[1]} \quad w_{3.1}^{[1]} \quad w_{4.1}^{[1]} \\w_{1.2}^{[1]} \quad w_{2.2}^{[1]} \quad w_{3.2}^{[1]} \quad w_{4.2}^{[1]}
\end{matrix}
\right]
+
\left[
\begin{matrix}
[b_1^{[1]} \\ b_2^{[1]} \\ [b_3^{[1]} \\ b_4^{[1]}
\end{matrix}
\right]^\mathrm T
=
\left[
\begin{matrix}
[z_1^{[1]}] \\ z_2^{[1]} \\ [z_3^{[1]}] \\ z_4^{[1]}
\end{matrix}
\right]^\mathrm T
\\\\
\left[
\begin{matrix}
a_1^{[1]}\\a_2^{[1]}\\a_3^{[1]}\\a_4^{[1]}
\end{matrix}
\right]^\mathrm T
·
\left[
\begin{matrix}
w_1^{[2]} \\
w_2^{[2]} \\
w_3^{[2]} \\
w_4^{[2]}
\end{matrix}
\right]
+
\left[
\begin{matrix}
b^{[2]}
\end{matrix}
\right]
=
\left[
\begin{matrix}
z^{[2]}
\end{matrix}
\right] \\\\
此时图形变化为:
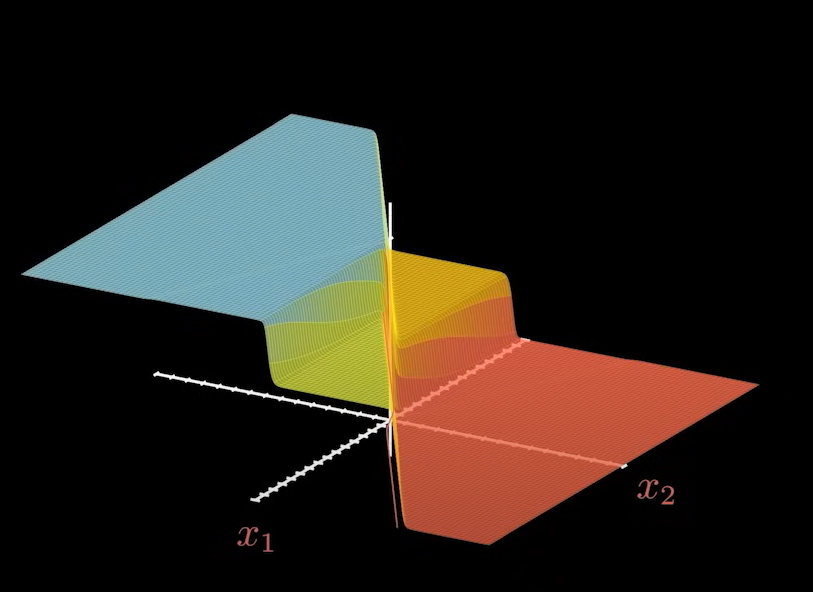
无论是输出结果的曲面,还是分界线,他们的复杂程度大大增加:
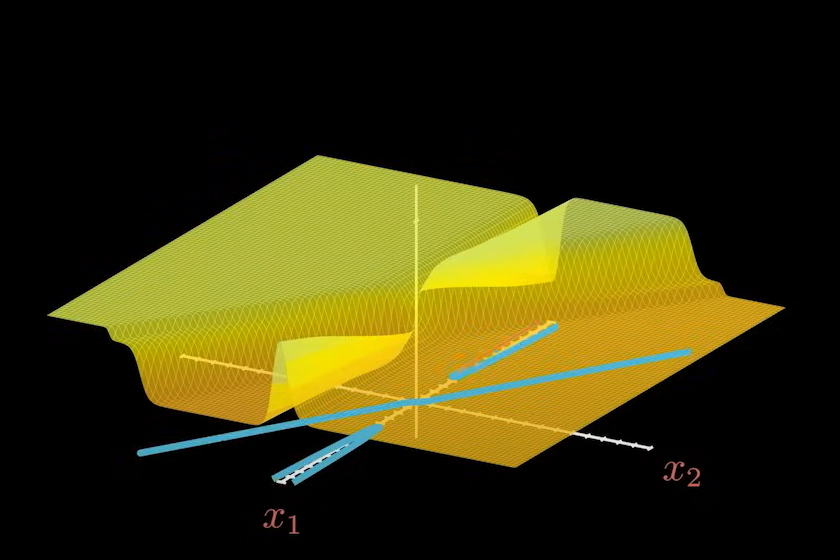
至此,我们持续增加神经元,图形的复杂程度会越来越高。
数据家也证明了,只要增加的神经元足够多,任何一种复杂的曲线都能够被无限的接近表达出来,即万能逼近定理(通用近似定理)。
神经网络要想实现万能逼近,其中有一个关键是激活函数。必须是非线性的,如果没有激活函数,再多的神经元也不会增加模型的复杂性。模型的图像只会是一个超平面。常用的激活函数如下:
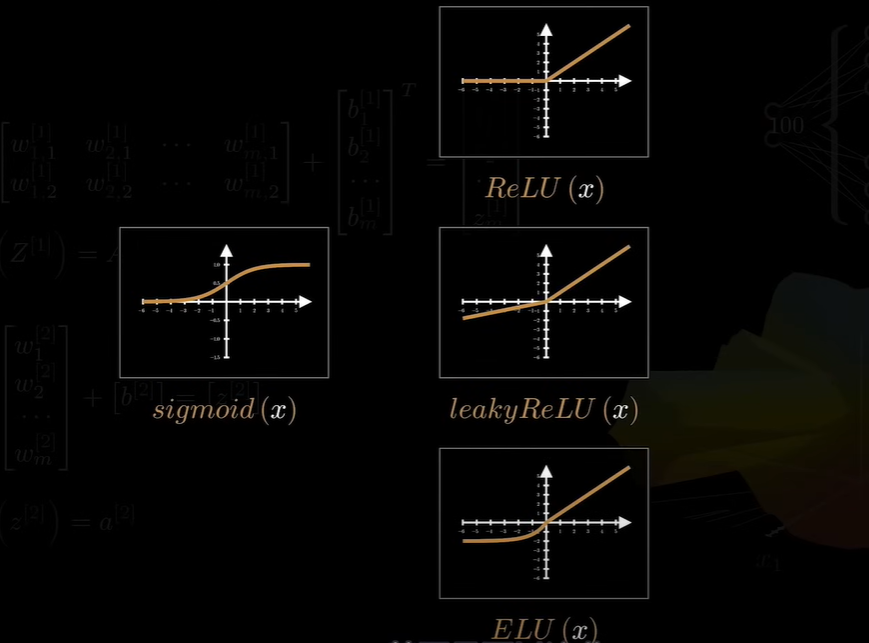
也可以是:sin(x) sinc(x) Gaussion(x) 。不同的激活函数对应的图形是非常不同的。
激活函数深入
为什么增加更多的神经元会有更强的能力,从另一个角度进行解释。
将前面神经网络部分看作为一个黑盒,不论输入的数据是什么样子,最终输出到最后一个神经元只是一个计算结果。假设他有 10 维。如图:
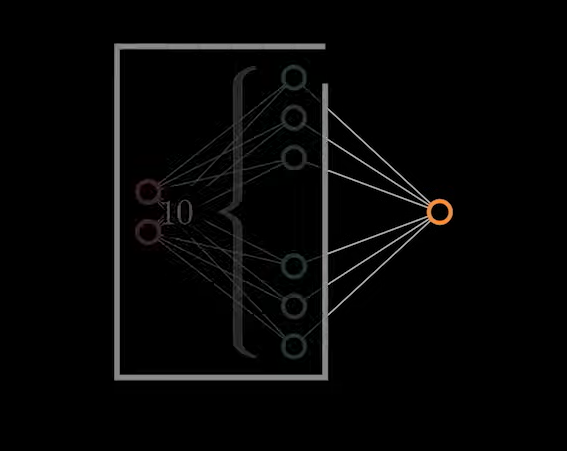
数据从2维到10维。其中的关键是数据的输入进行了一个矩阵运算,矩阵对一个向量进行操作。将其变为另外一个向量:
例如如下的向量:
\left[
\begin{matrix}
1\\1
\end{matrix}
\right]
进行如下的运算:
\left[
\begin{matrix}
1\\1
\end{matrix}
\right]
·
\left[
\begin{matrix}
cos\theta \quad -sin\theta\\sin\theta \quad cos\theta
\end{matrix}
\right]
将向量旋转 θ 角度:
那么这个矩阵的作用就是使向量发生旋转。
那么如下的矩阵,完全可以起到对向量进行升维的作用:
\left[
\begin{matrix}
1\\1
\end{matrix}
\right]
·
\left[
\begin{matrix}
w_{1.1} \quad w_{2.1} \quad w_{3.1} \\
w_{1.2} \quad w_{2.2} \quad w_{3.2}
\end{matrix}
\right]
如果数据只是二维的,它们互相参杂在一起,很难直接用直线对数据进行划分:
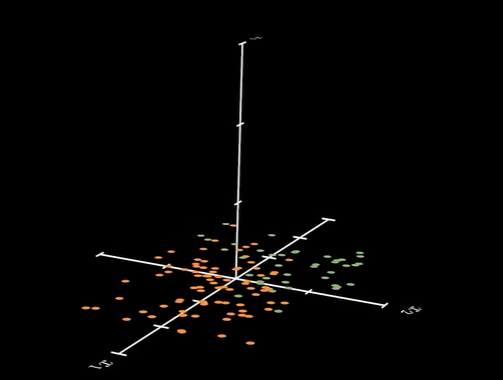
如果对它们进行升维:
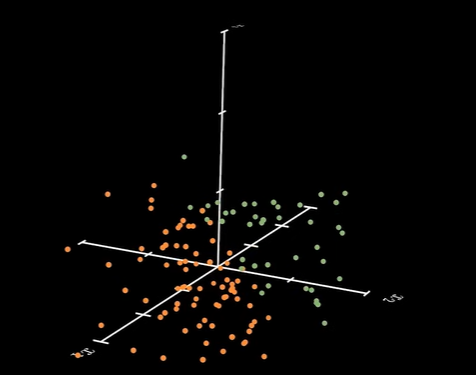
用跟简单的模型也可以将他们分开:
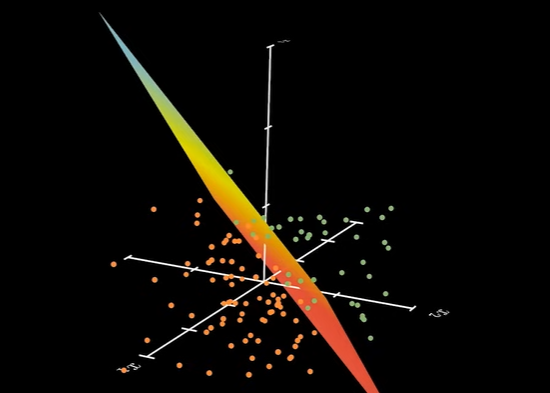
因此,我们可以把神经元中中间的操作看作是数据升维的操作:
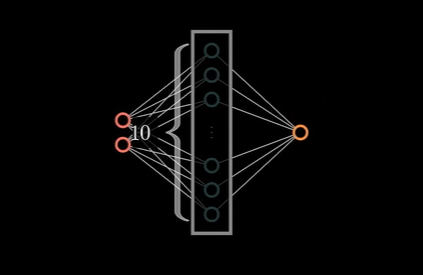
有多少神经元,就会把数据升到多少维。只要维度够高,一定会找到一个超平面,能对数据完成划分。
这样就变成了我们之前讨论的 f(x) 问题:
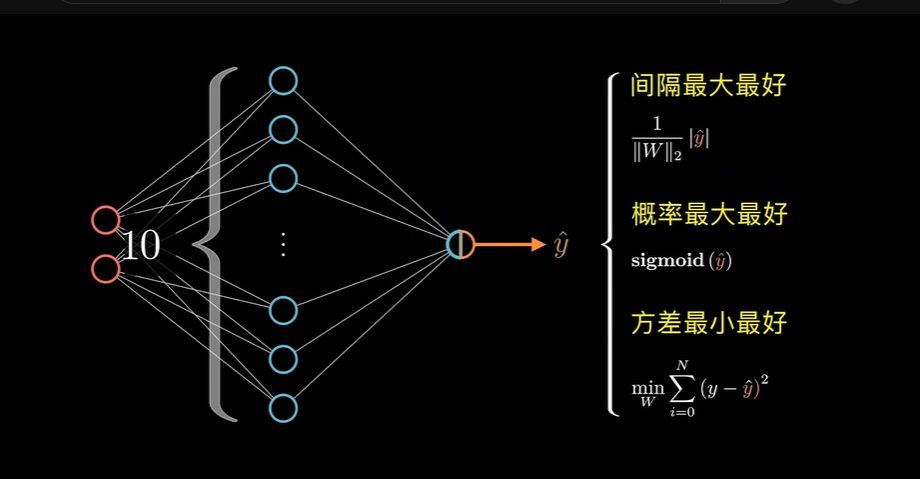
多分类问题
一个神经网络并不是只能有一个输出节点,处理二分类问题。也可以有多个节点,进行多分类问题的讨论:
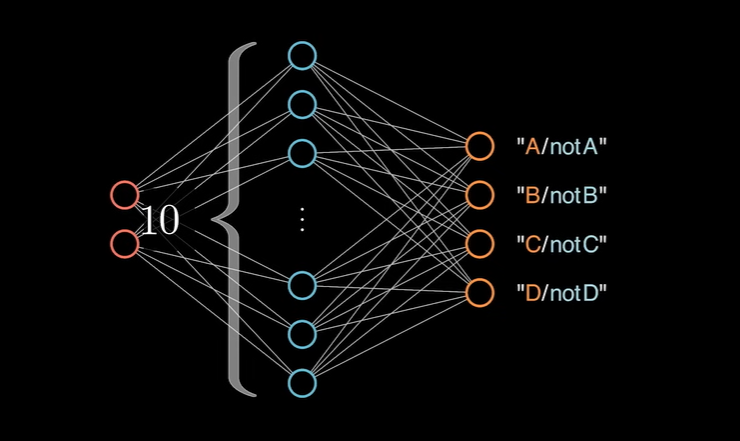
其实质也是在每一个输出节点上进行二分类判断,将各个节点综合起来,就可以去解决多分类问题。真实的场景中,并不像是上述描述的粗糙,而是通过 softMax(Y)函数进行统一描述。函数表达式如下:
softMax(\hat{Y}) = \frac{e^{\hat{y_i}}}{\sum_{j=1}^4e^{\hat{y_j}}}
就是对 singmoid(x) 函数的扩展和升级。
完整的神经网络如下:
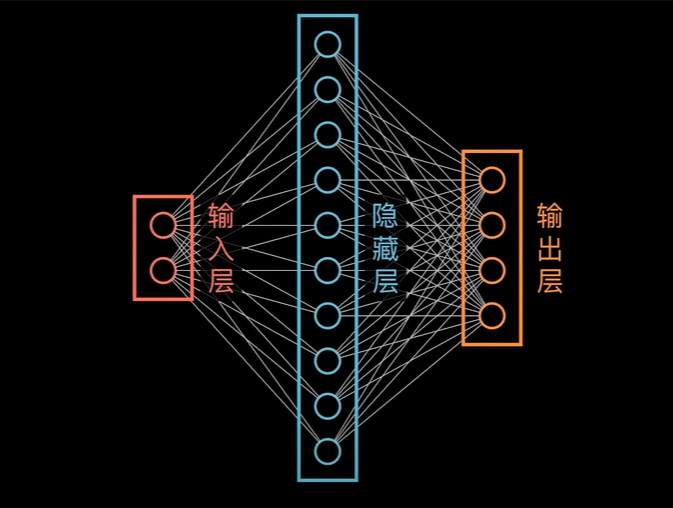
这里的隐藏层暂时理解为对数据进行升维操作。不过更常见的神经网络应该是如下的表示:
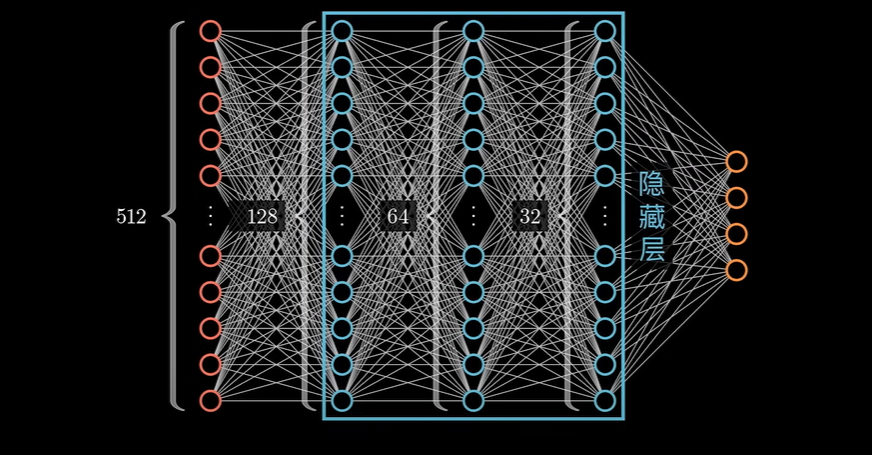
基于如上的神经网络,继续使用隐藏层就是对数据升维的看法,就会出现问题,从左到右,神经元的个数在递减。我们仍然回归到简单问题:
神经网络的输入输出可以是:
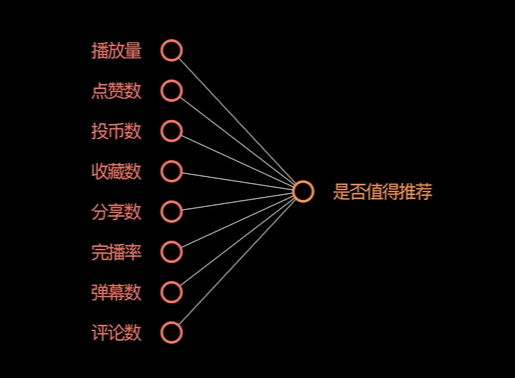
基于上述神经网络很难有新的发现,我们只需要将问题换成下述这样,就会有新的发现:
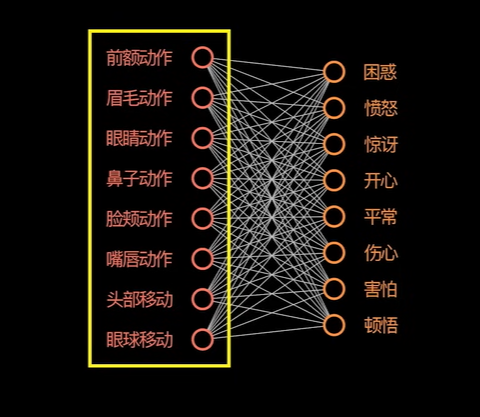
案例分析 - 判断面部表情 & OCR
上述的数据维度完全可以看作是判断一个人心情的特征。在现实生活中,可没有这么清晰的输入数据去让模型进行判断。而在现实生活中存在可能是这样的一张原始图片:

图片上的每一个像素都是数据的一个维度:
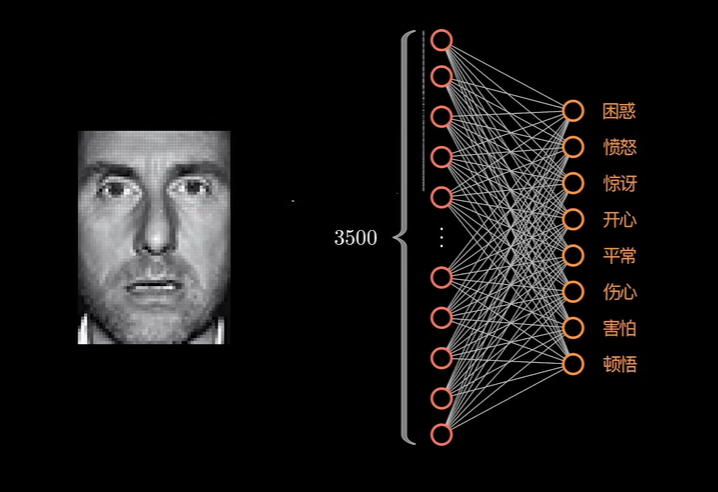
这时候在加入隐藏层:
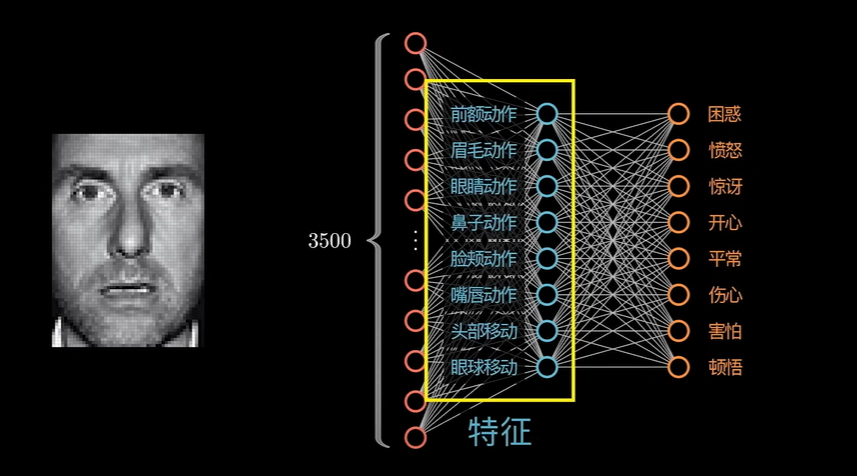
就可以理解成人类面部表情的特征。
为什么这里反而降维了呢?这是因为这里的一个特征,并不需要原始数据里的所有维度。例如眼睛的动作,我们完全可以只关注眼镜的像素点。
这里隐藏层就可以理解成对上一层原始数据的抽象。
如果只是到此程度的话,还是不能有效的解释为什么神经网络需要这么多层。这时候如果我们换个问题继续理解,就会明白。
比如我们需要使用神经网络去判断手写的数字:
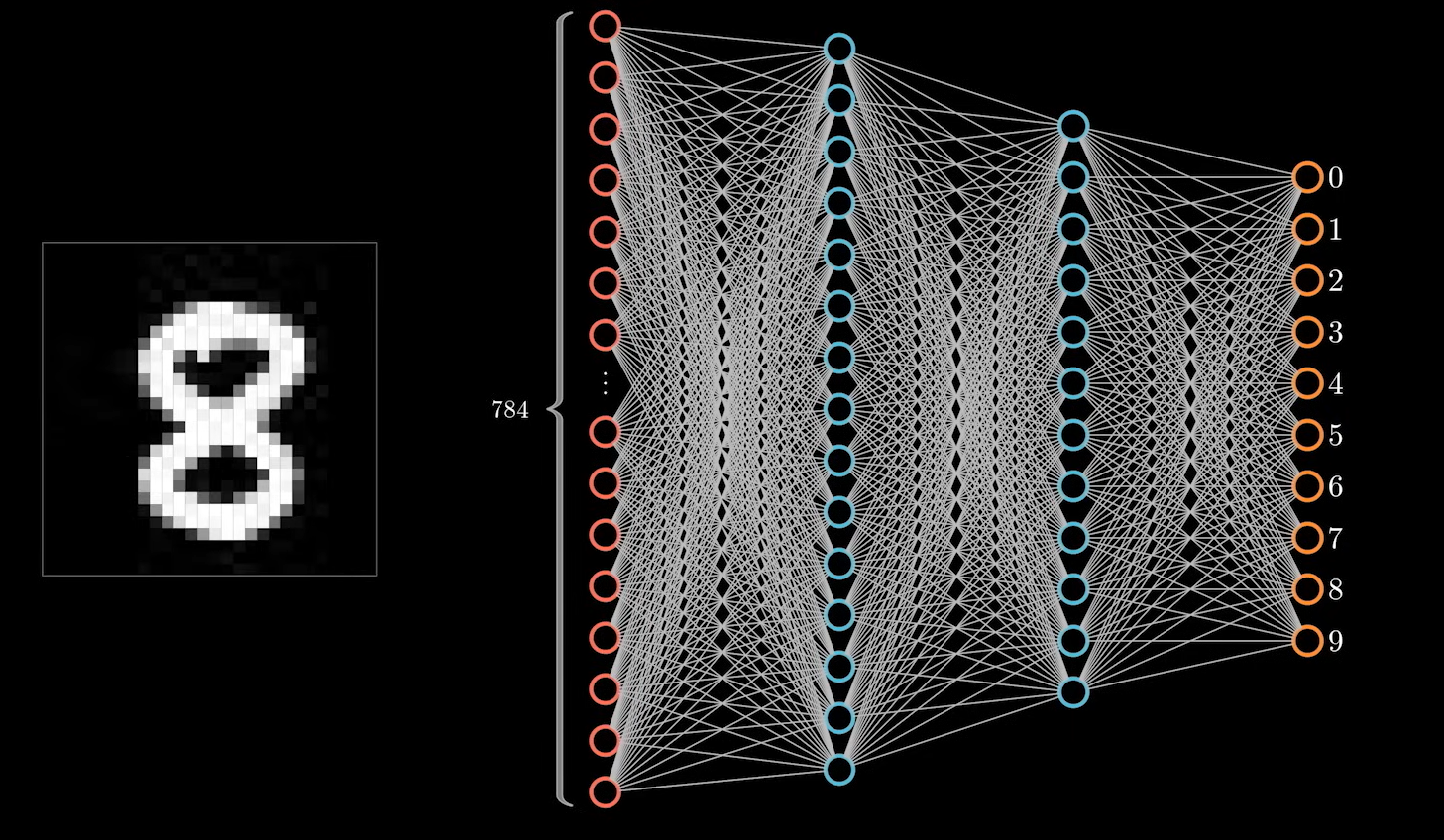
比如数字 8 ,神经网络很可能会将 8 上下两部分的特征提取出来作为判断的依据。如图:
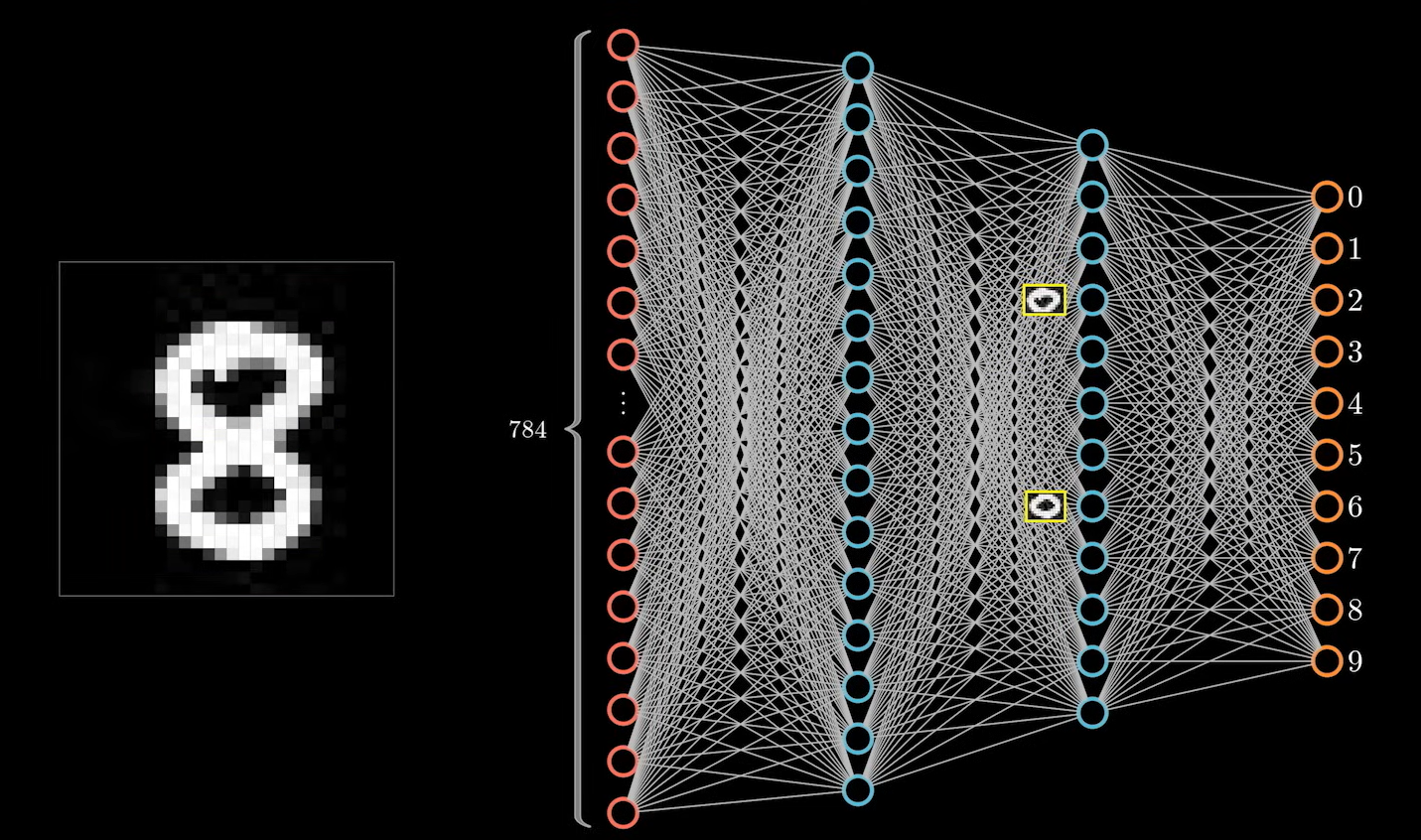
这里将其放在第二个隐藏层的原因是,两个圆可能还有其自己的子特征:
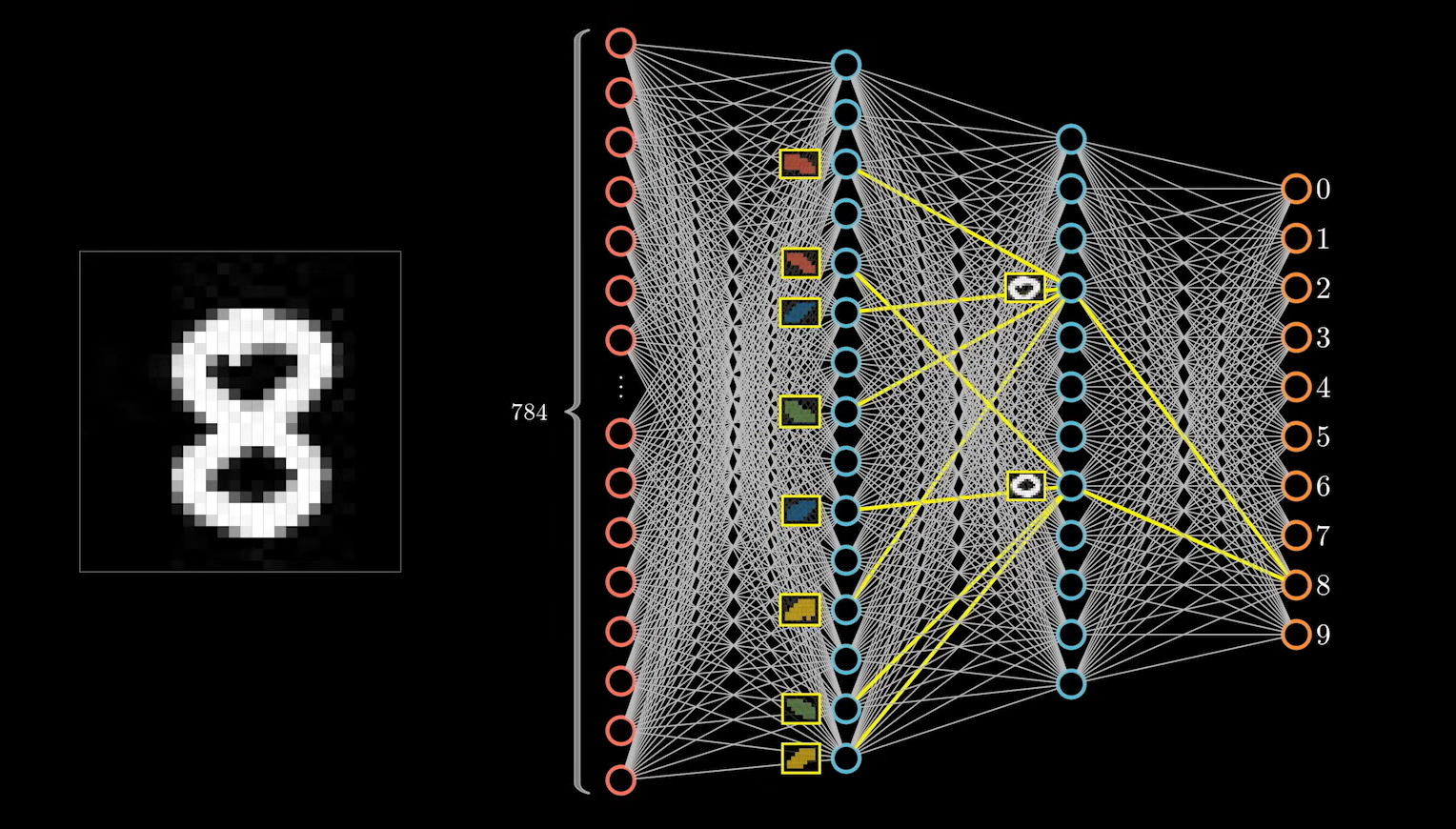
他们都由四部分圆弧组成。这样做的好处是在遇到同样的特征时可以复用,比如数字 6 ,下半部分也是一个圆圈的结构,下面的特征就可以和 8 进行复用。
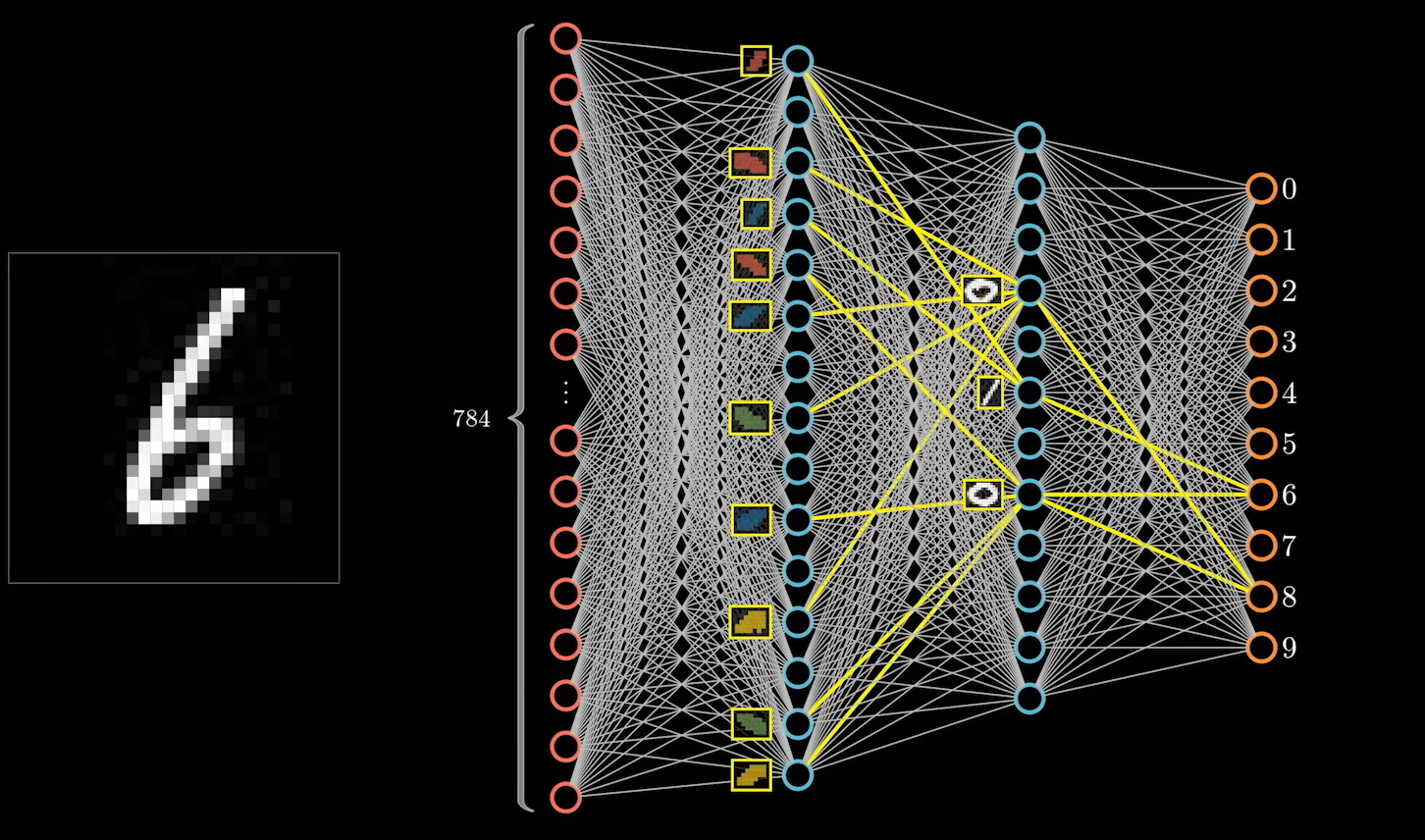
上半部分的一竖才是数字 6 独有的特征。
对应的数字 5 ,下半部分是半个圆弧,同样也可以进行复用,不同的特征只有上面的 一横 这一部分。
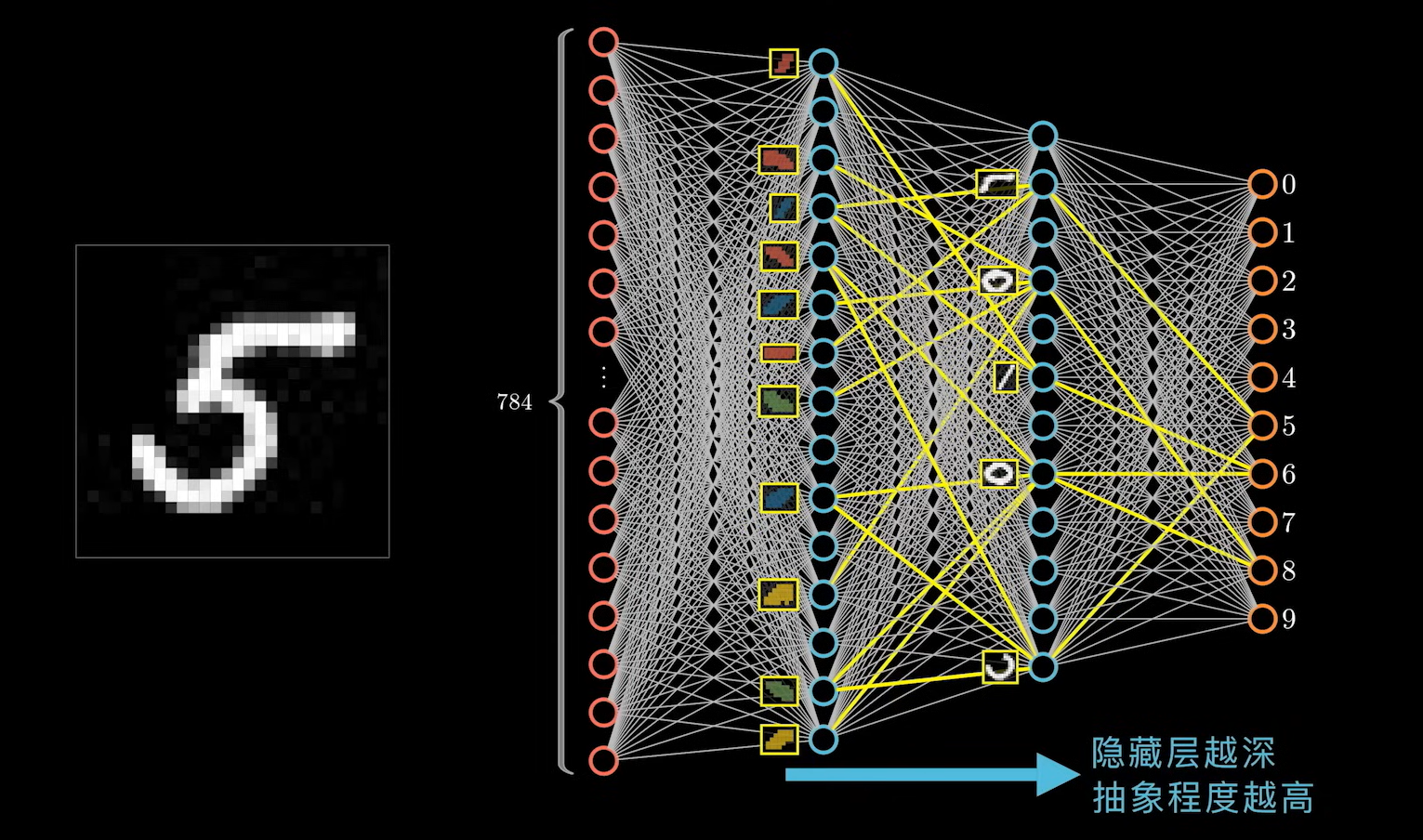
对神经网络的层数可以理解为:隐藏层越深,对数据的抽象程度越高。
这里只是用了我们人能理解的特征进行描述,神经网络自己学习到的特征,可能人无法理解,但是预测结果同样十分准确。
上述的就是对一个完整的神经网络的描述。
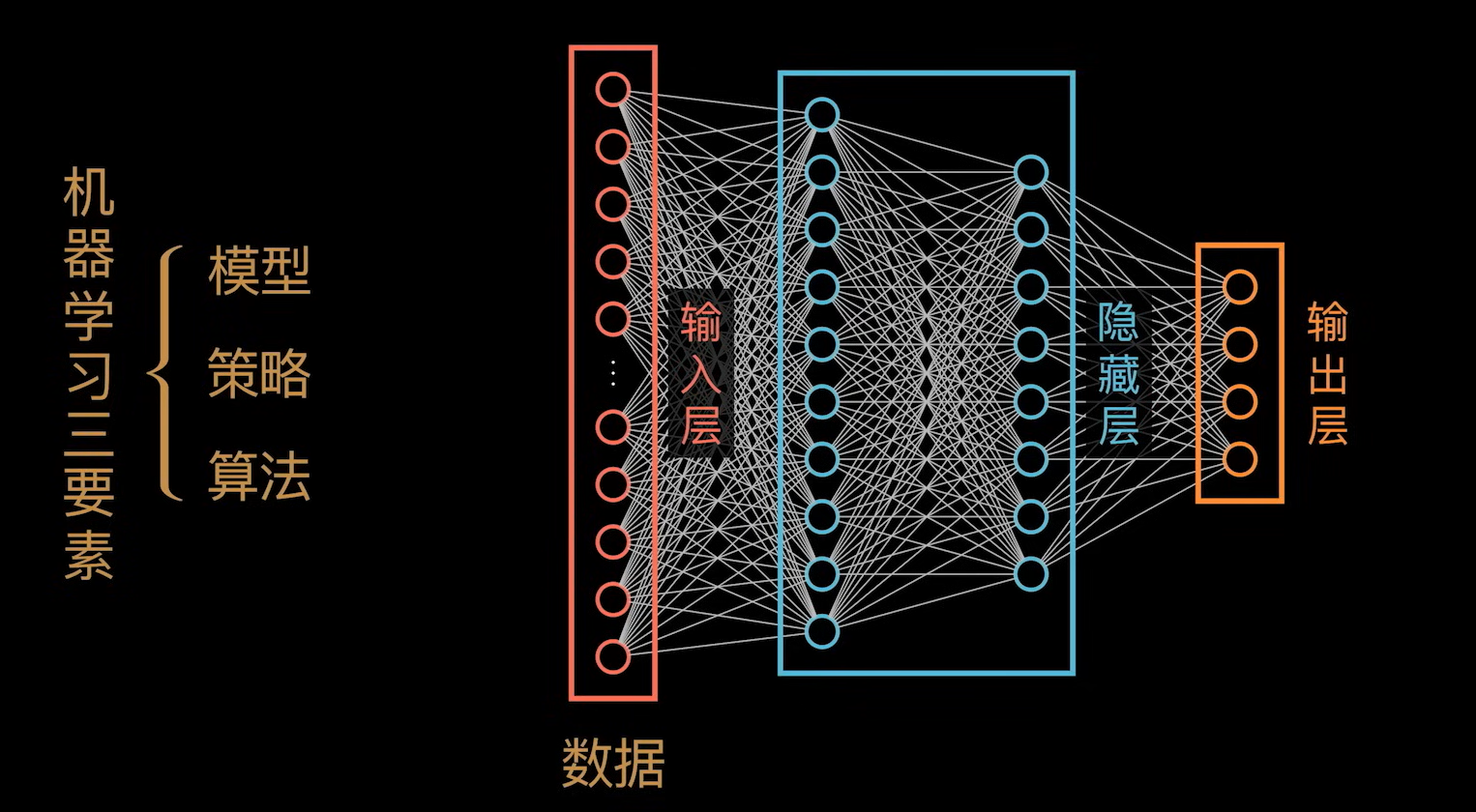
模型 -> 隐藏层
策略 -> 输出层
其实在输入层也需要对数据进行预处理。随着算力需求越来越大,如何对数据进行预处理使其得到最佳结果。也是一个非常重要的问题。
算法 - 梯度下降算法
在神经网络中,这个算法没有别的,就是反向传播(梯度下降)算法。
算法推导
一个神经网络我们完全看作是一个这样的函数:
f_w(X) = \hat{Y}
只不过这个函数相当复杂而已。如果神经网络已经训练成功,在进行判断和决策的时候,他们的输入就是 X 系数 W 是作为参数。这个过程称之为正向传播。但是,如果一个神经网络正在被训练,他们之间的关系就会变得相关。
f_X(W) = \hat{Y}
x 作为已知的参数,系数作为变量,是需要求解的。因此,函数的图像也会发生相应的变化。如图为一个正向传播的函数图像:
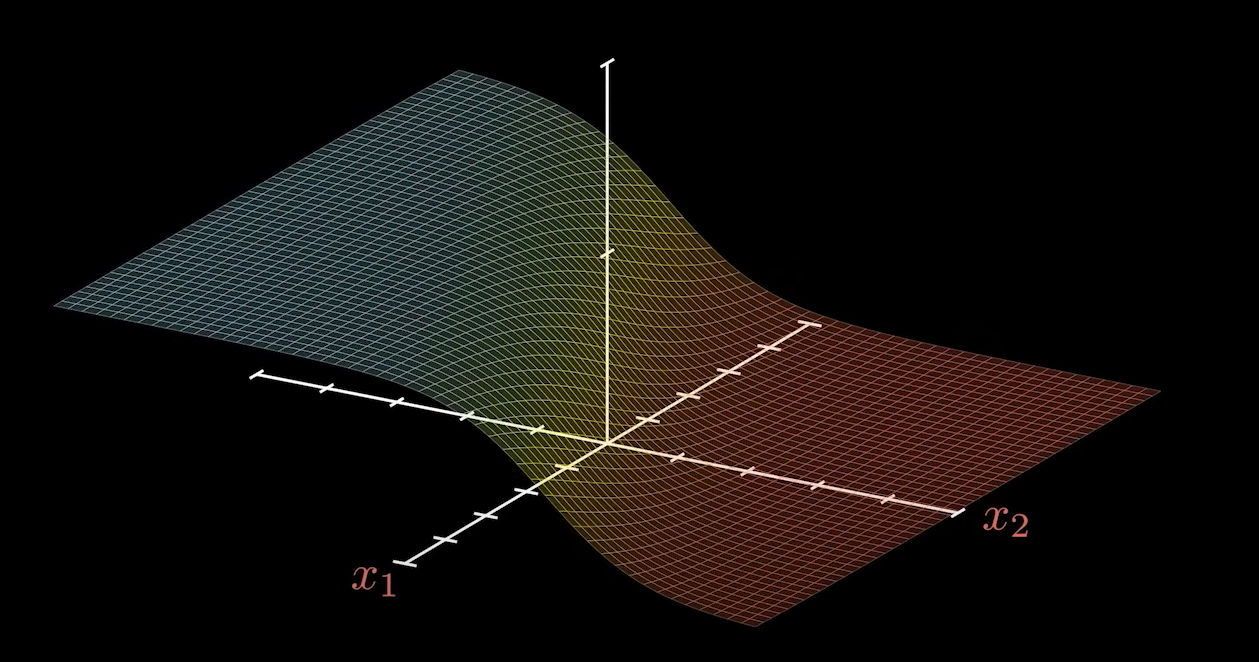
如果将系数 W 看作变量的话,坐标不再是 x1 和 x2 而是 w1 和 w2。
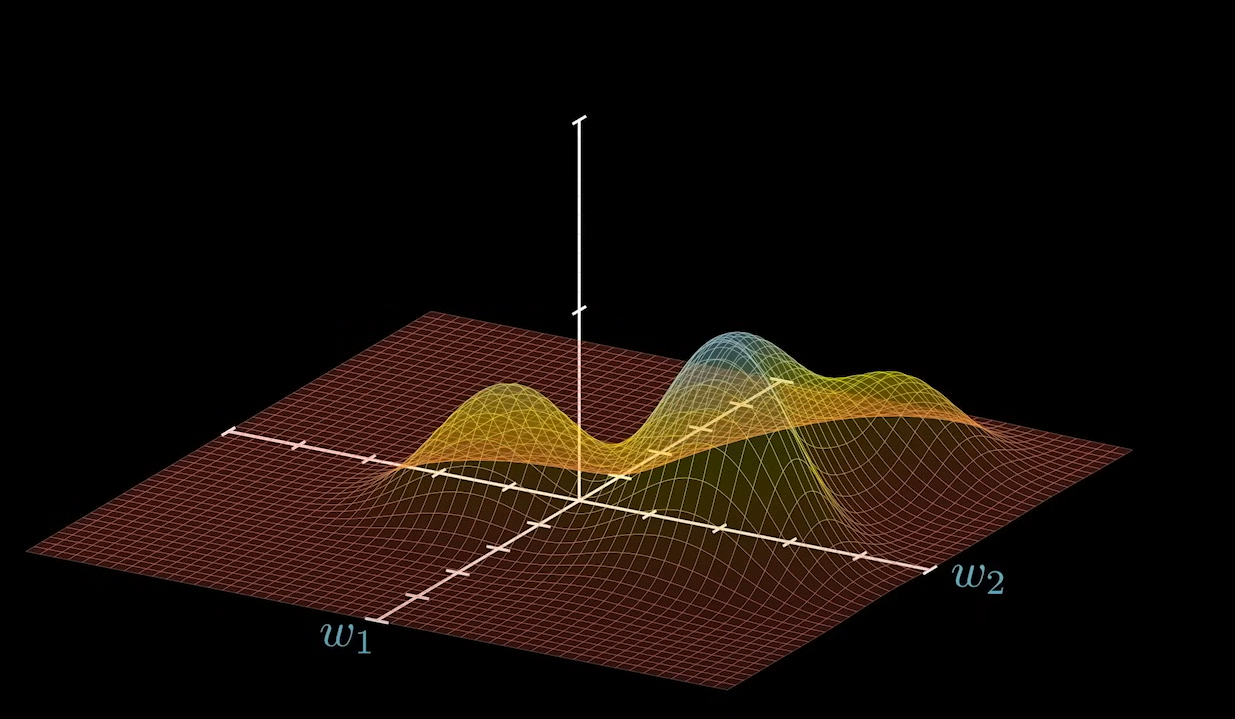
上图为一个简化处理,这里我们假设不知道神经网络的具体情况,只是将 所有的系数看成是一个向量。后面我们会修正图像。这里的最高点就是我们在选择策略后希望出现的结果。
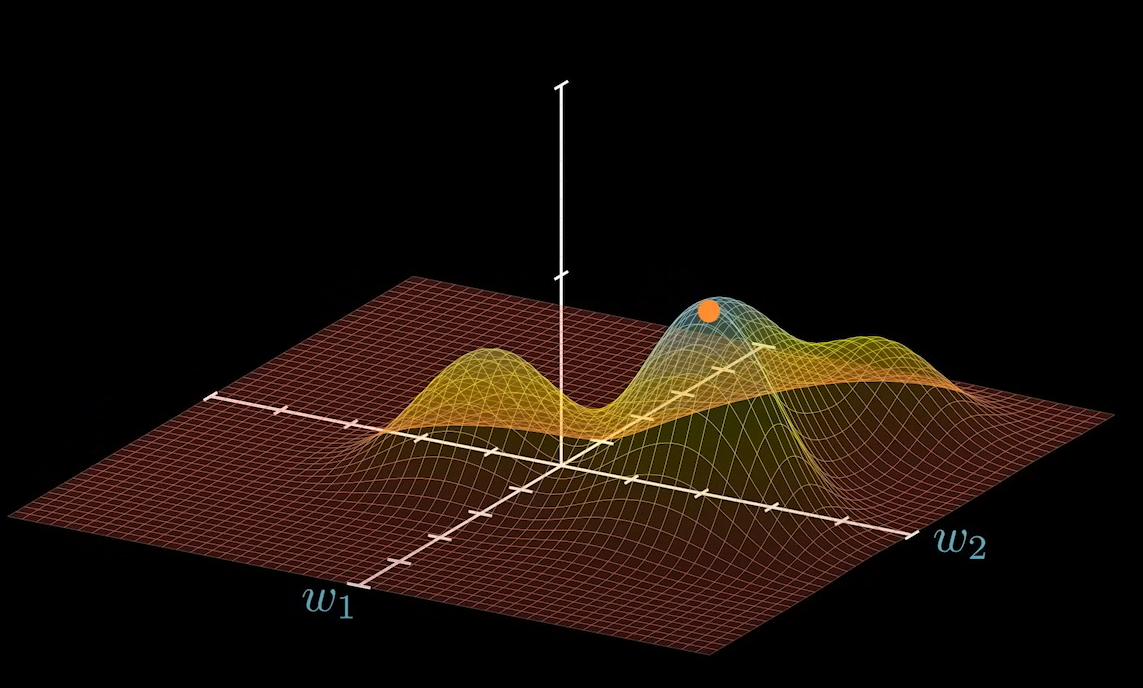
我们这里的结果不是求出 Y 的值,而是求出令 Y 最大时 W 的取值。
这个 W 的取值就是最高点在系数平面上的投影:
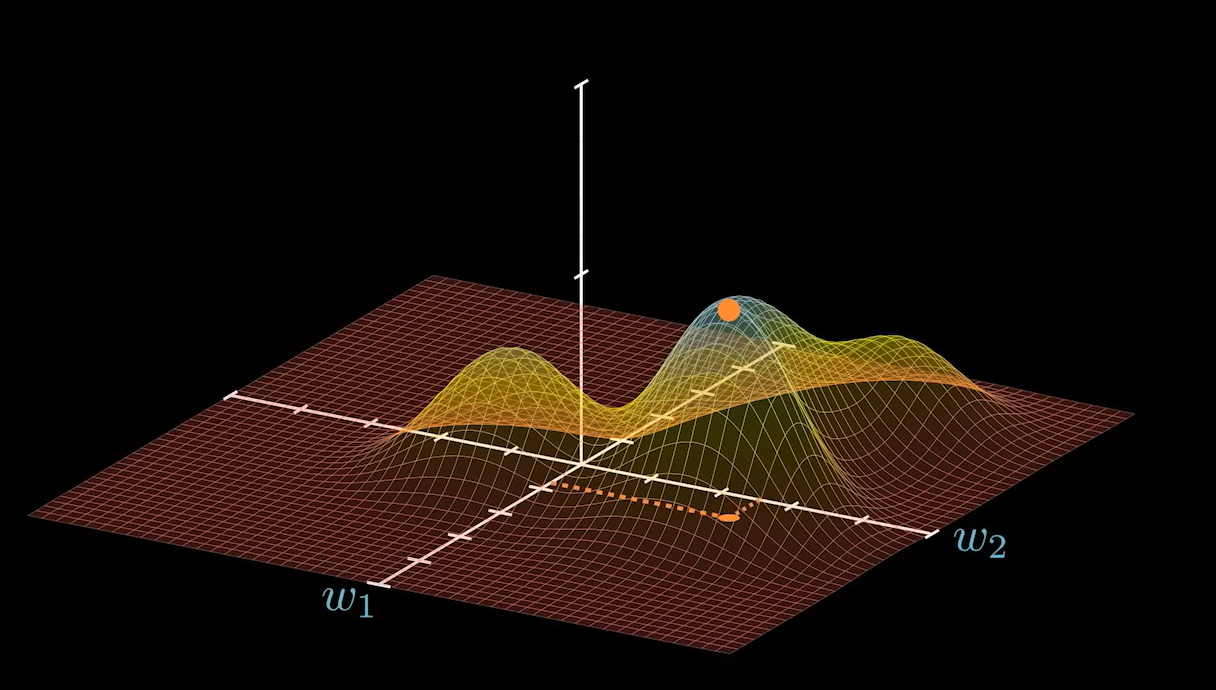
不过,我们在初始化一个神经网络的时候,系数 W 可能出现在任何一个位置,理想情况下,他到最优点的距离就是我们求解的目标:
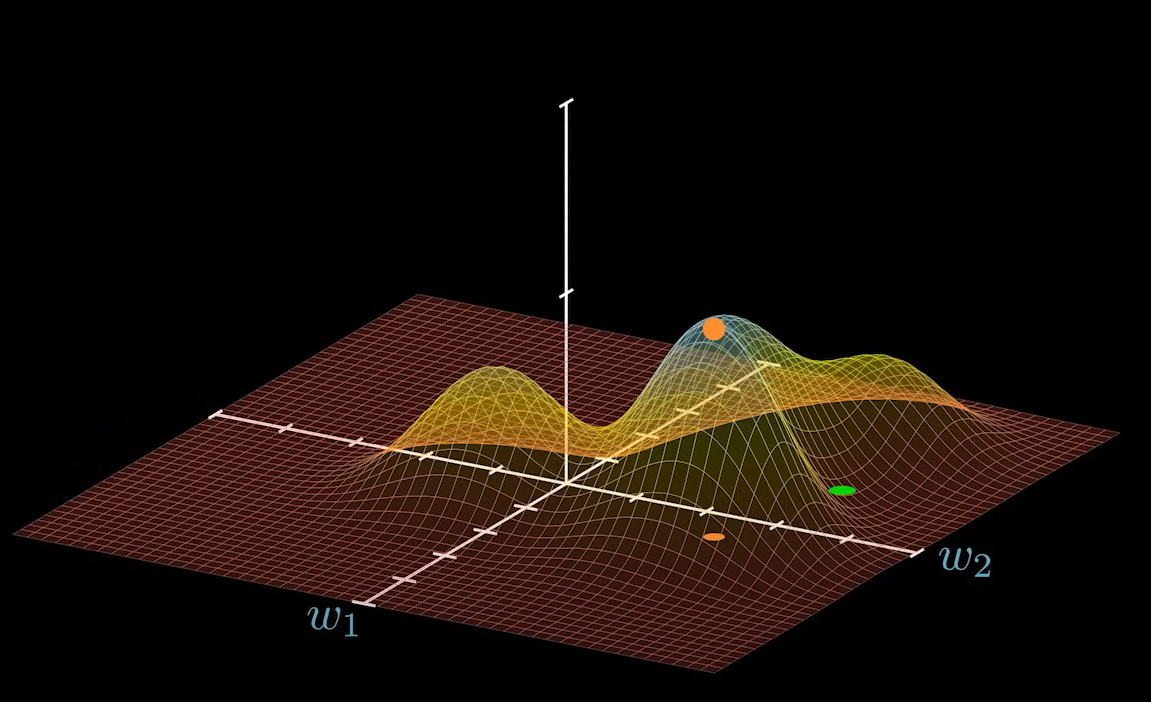
f_x(W^*) = \hat{Y_*}
W - W^* = \Delta W
但是在实际场景,上述 W 的值很难直接计算出来。如果利用如下的方式,我们就可以求出:
在曲面上的任意一点:都可以求出一个向量:
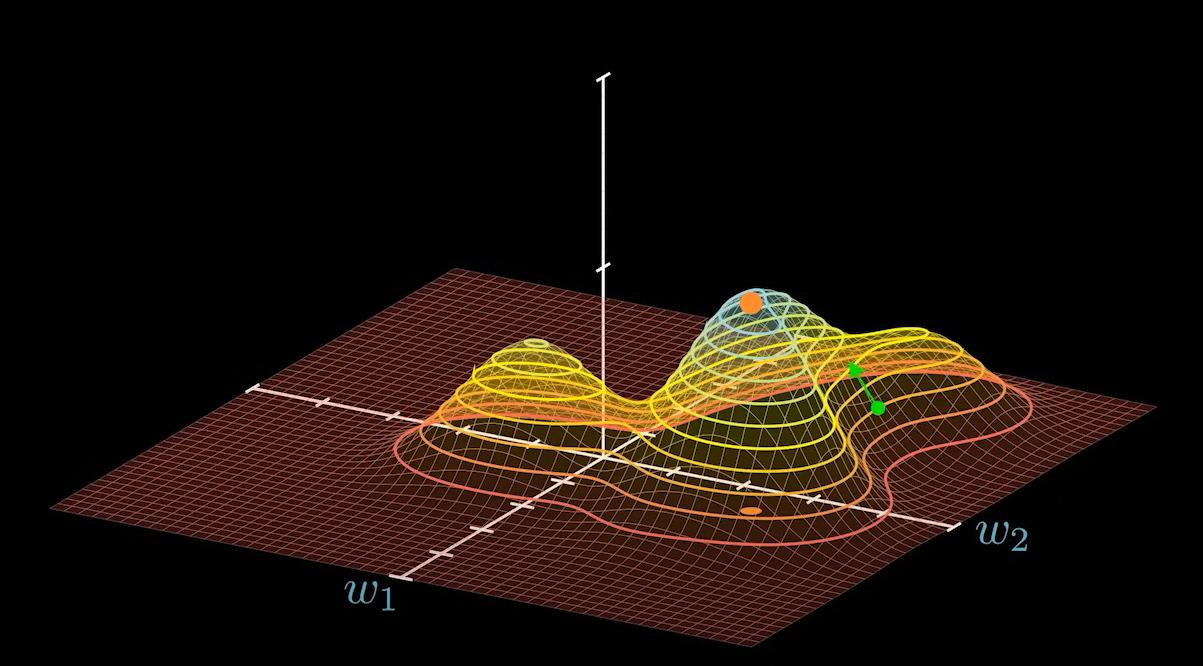
这个向量总是指向上升最快的方向:
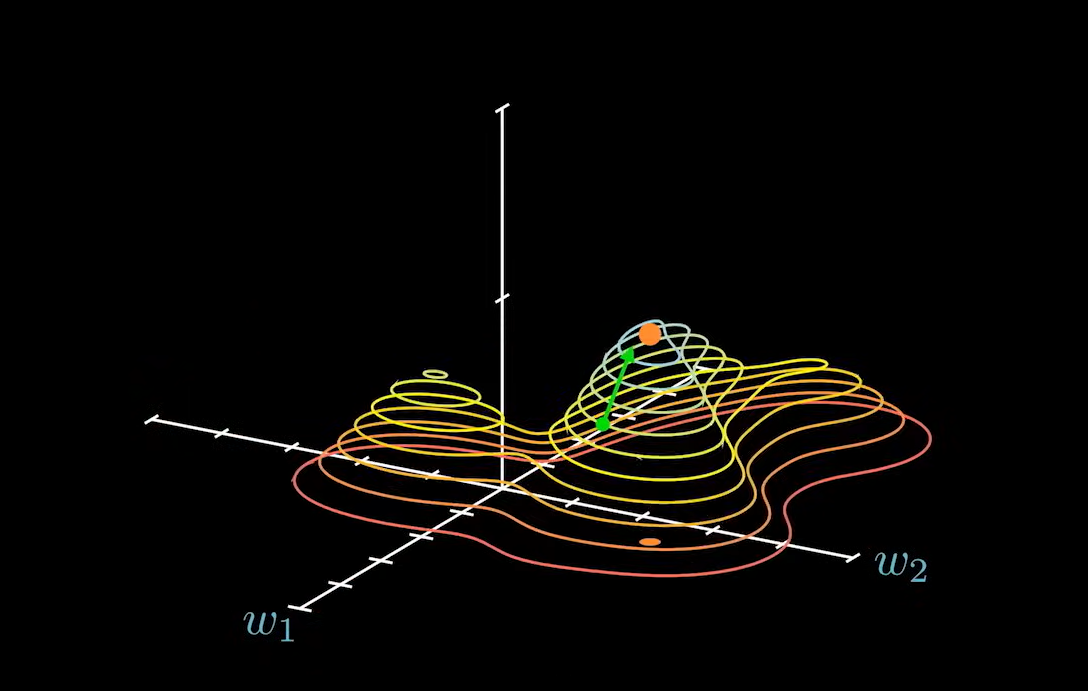
那么这个向量在参数平面上的投影就叫做 梯度。
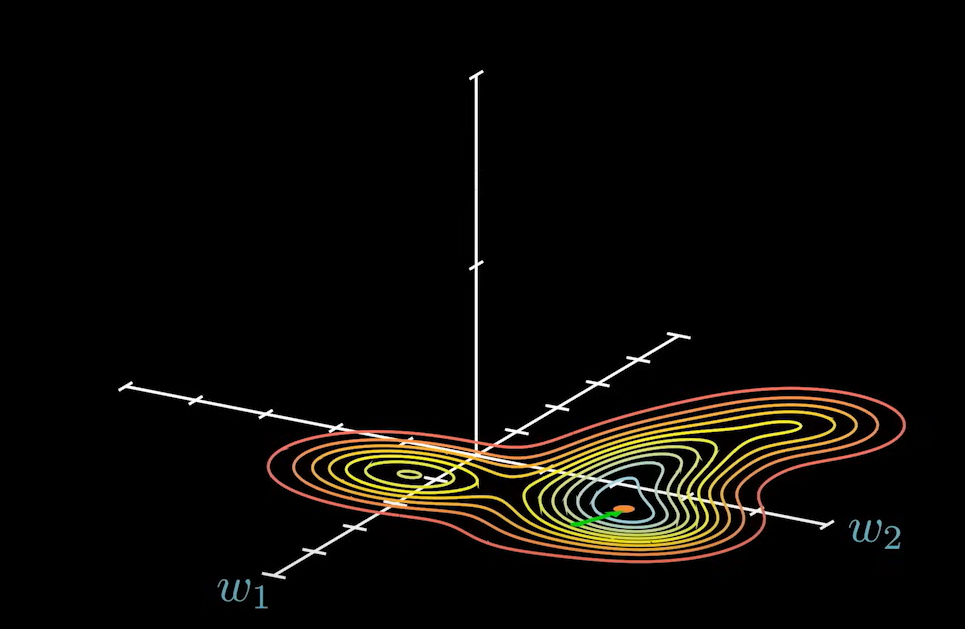
梯度总是指向上升最快的方向,那么为何称为梯度下降法呢?在选择策略的时候,有的策略是求最大,有的是求最小。为了将其统一看待,即便是求最大的问题,我们也可以在其上加上负号使其变成求最小的问题。
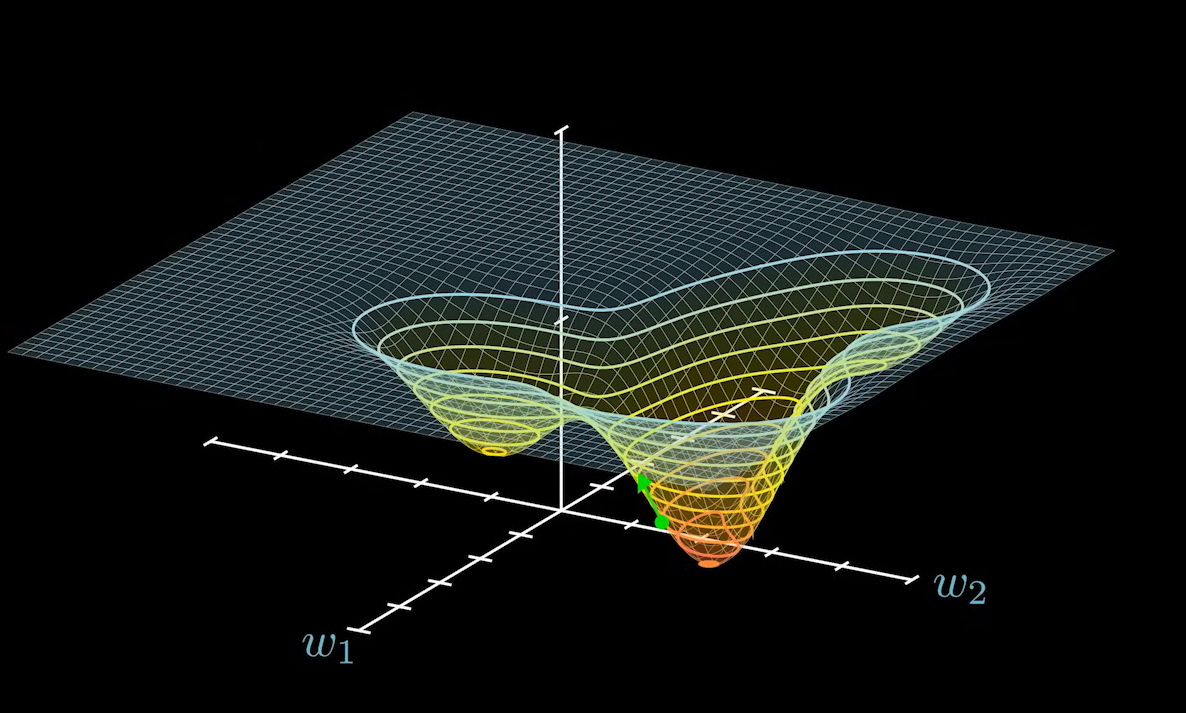
不过虽然的这里曲面反了,但是梯度仍然是指向上升最快的方向。所以在具体操作的时候,会对梯度先求反,这样梯度就会指向下降最快的方向。这就是这个算法 梯度下降法的由来,不过其本质仍然相同。
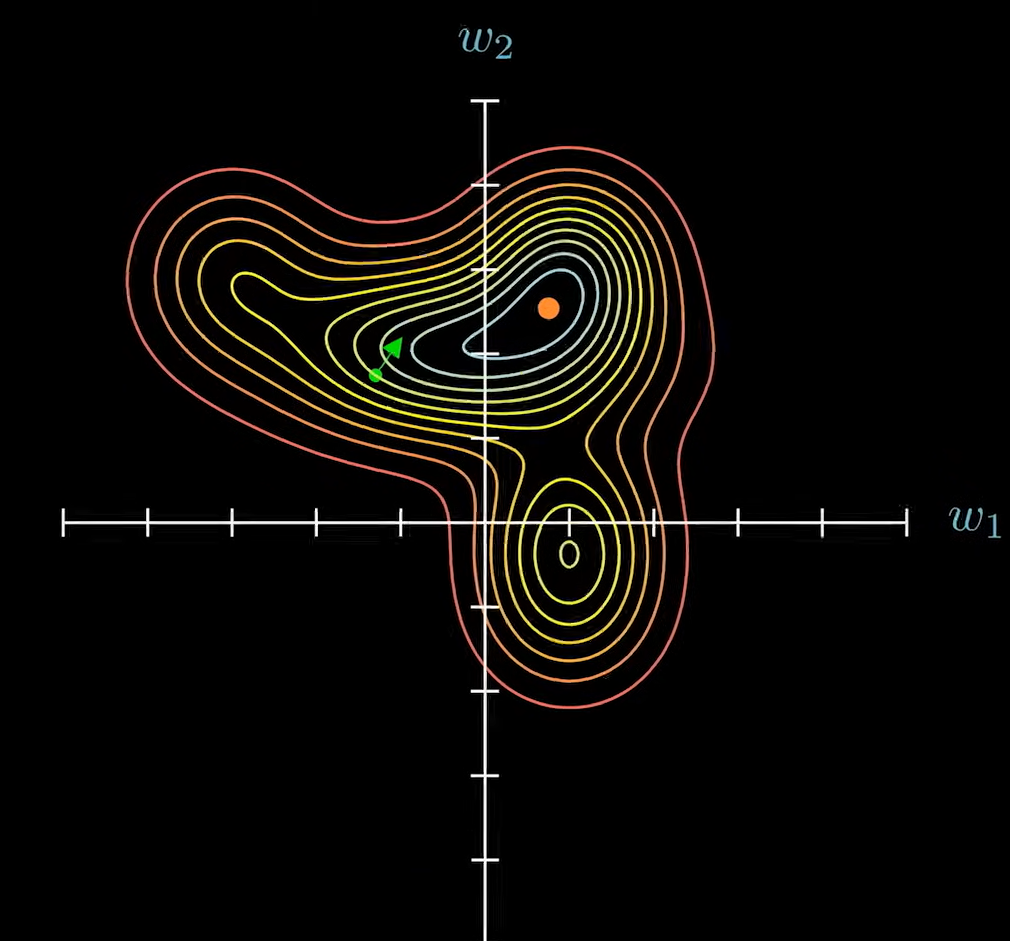
梯度下降法在模型中的应用
梯度总是指向上升最快的方向,即总是和等高线垂直。梯度本身是一个向量,所以就代表了他在所有参数维度上都有分量。
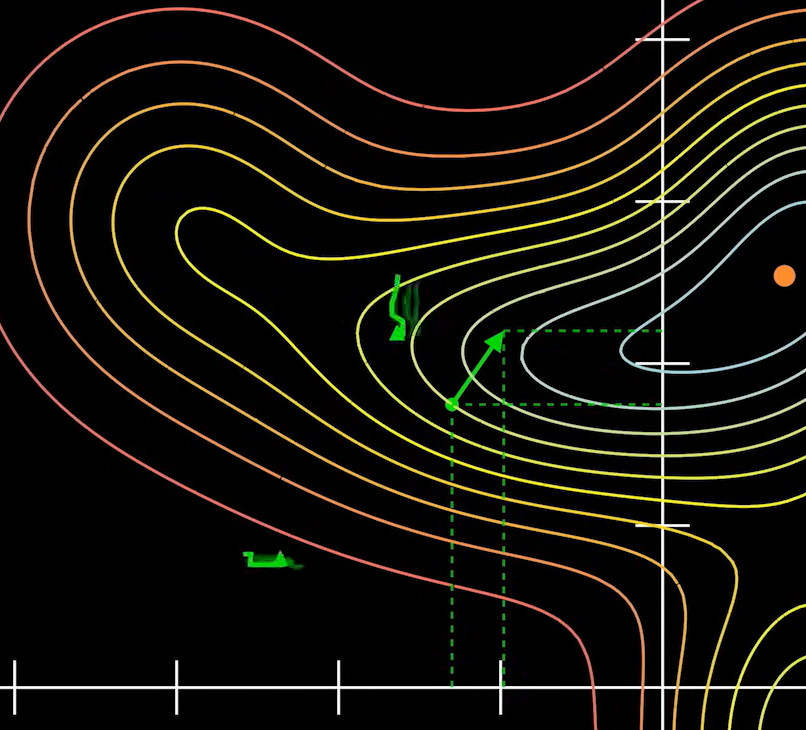
如果所有的参数都按照梯度的分量进行调整,这样就代表参数 W 做出了当前情况下最好的选择。
\left[
\begin{matrix}
w_1\\w_2 \\ \cdots
\end{matrix}
\right]
\pm
\left[
\begin{matrix}
\Delta{w_1}\\\Delta{w_2} \\ \cdots
\end{matrix}
\right]
一次次慢慢移动,总会接近其级值点。
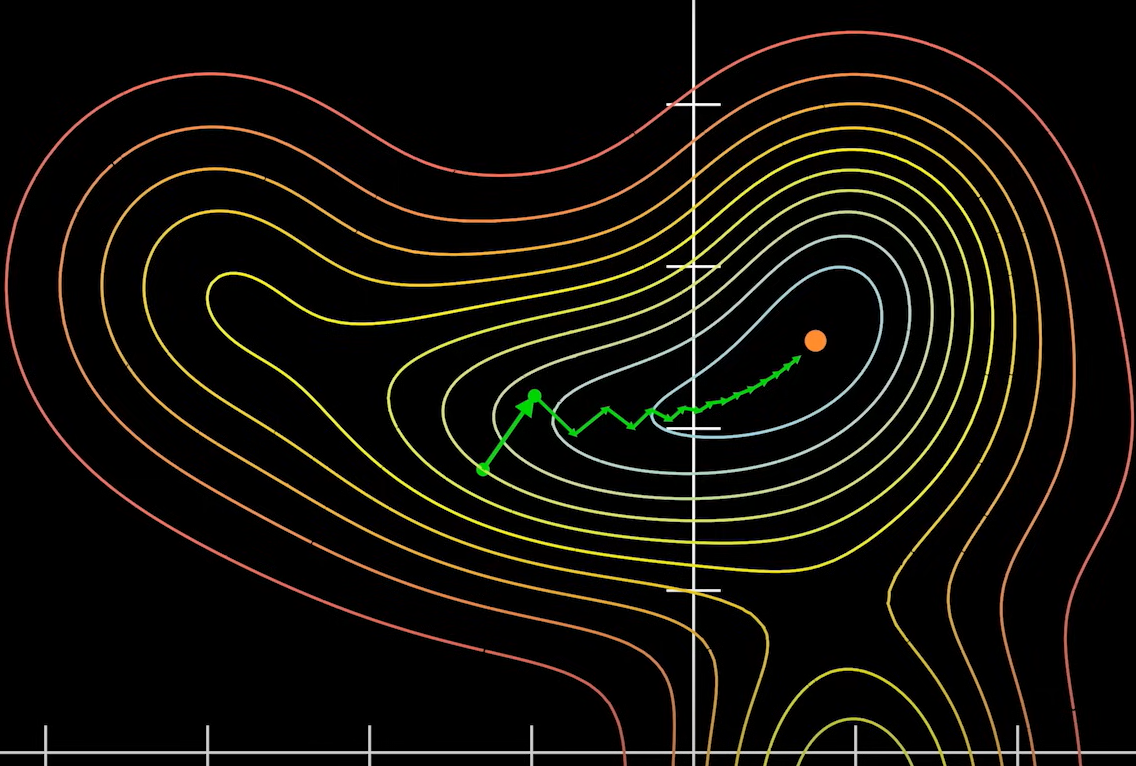
即便在这样的场景下,仍然存在问题,梯度只是指向了上升最快的方向,而没有指出其上升时每一步的步长。
步长在梯度下降法中通常用 η 来表示,也就是通常所说的学习率了。
\left[
\begin{matrix}
w_1\\w_2 \\ \cdots \\ \cdots
\end{matrix}
\right]
\pm
\eta ·
\left[
\begin{matrix}
\Delta{w_1}\\\Delta{w_2} \\ \cdots \\ \cdots
\end{matrix}
\right]
它是一个超参数,不能由神经网络学习得到,需要手动进行配置。
η 过大就会很快接近极值点,但是会造成反复横跳,无法收敛的结果。
η 过小,整体路径最优,移动相同次数,移动距离会比较短。
现在已经有了很多梯度下降的进阶方案。
算法实践
现在我们已经理解了其思路,如何求出梯度?就是如何求出分量的具体值。如果非常笼统的看待:求梯度的答案为对函数求偏导。每一个变量的维度都要求偏导。
\left[
\begin{matrix}
w_1\\w_2 \\ \cdots \\ \cdots
\end{matrix}
\right]
\pm
\eta ·
\left[
\begin{matrix}
\frac{\partial{f}}{\partial{w_1}}\\\frac{\partial{f}}{\partial{w_2}}\\ \cdots \\ \cdots
\end{matrix}
\right]
上述中的梯度也可以用 ∇f 表示,读作 nablaf。
接下来的问题是具体如何求出偏导。如果我们把神经网络整体看作是一个黑盒。
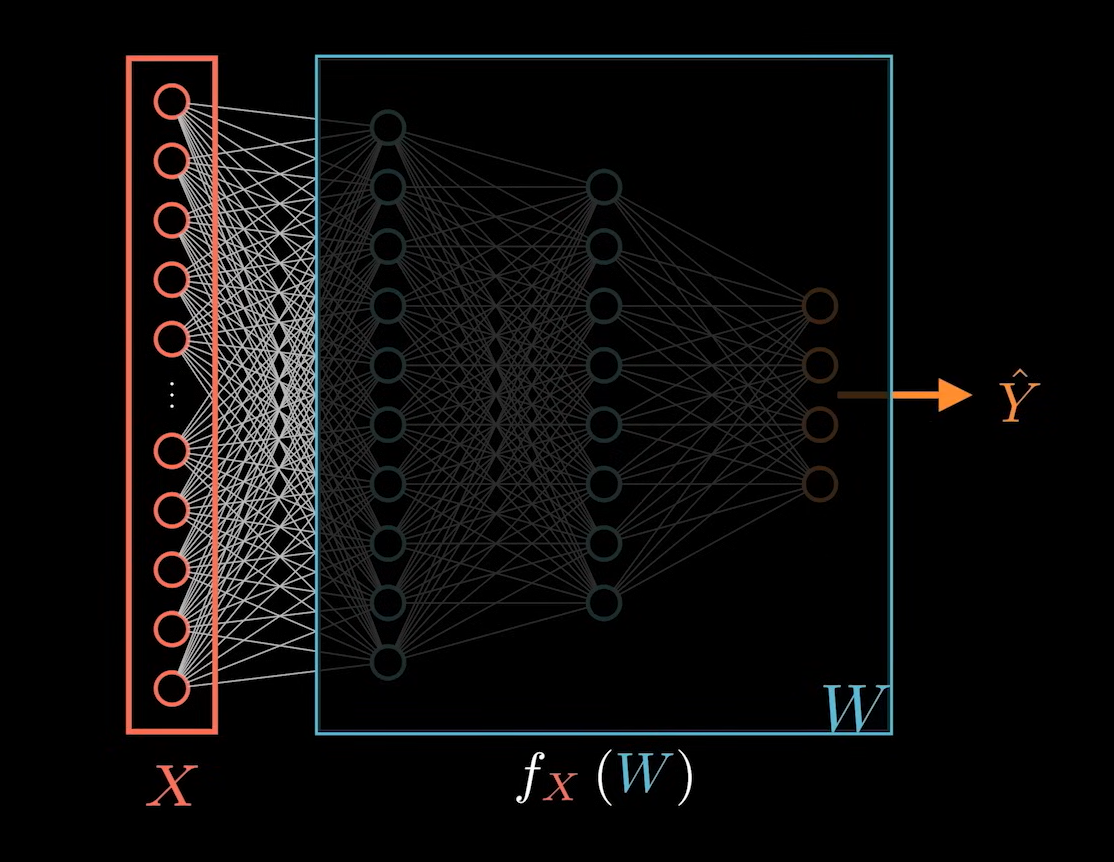
输入层是 X 不同的系数 W 对应不同的 Y 值。w 全部在黑盒中。
所谓的梯度下降便是:将计算出来的梯度反向传播到神经网络中,让所有的 W 进行修改。
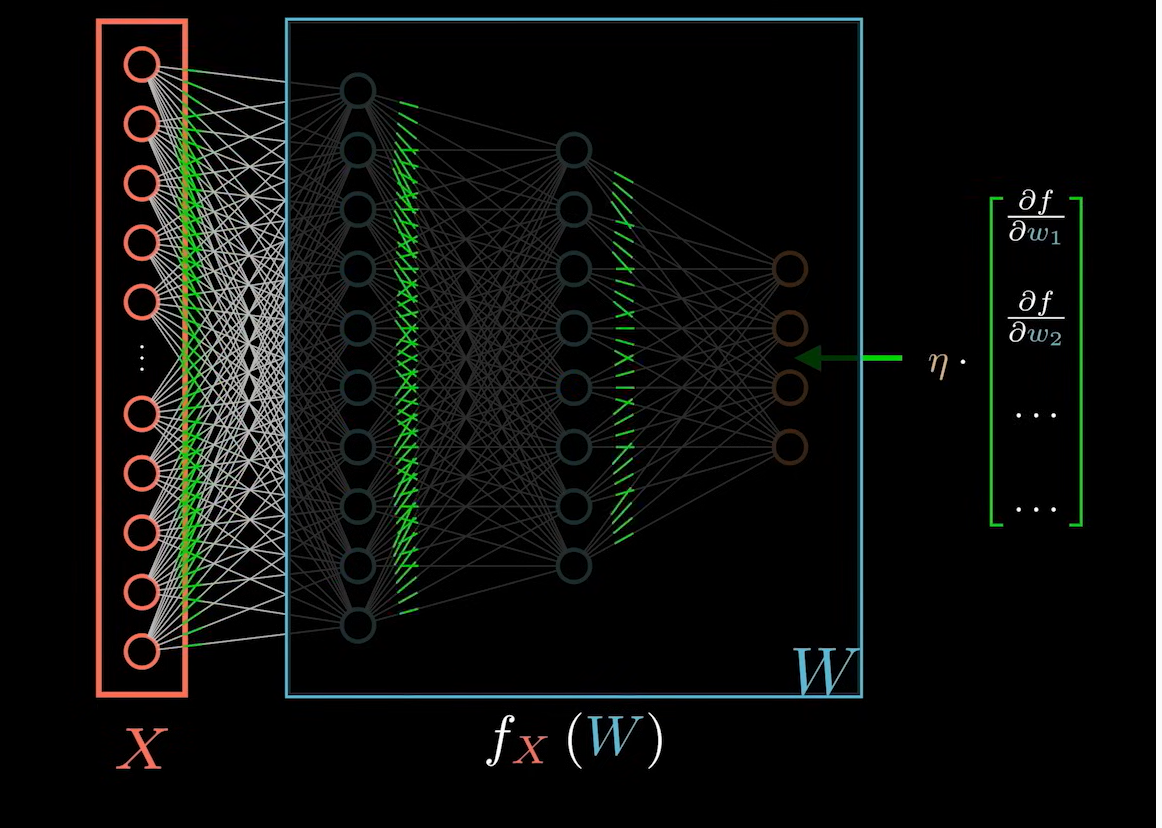
对于神经网络麻烦的一点是:不同的 W 之间是存在依赖关系的,不是单独存在。这个依赖关系就是神经网络的结构图。因此要想计算出每个系数对应梯度的分量还需要将黑盒拆开才行。那么,这个黑盒里面到底是什么?
其本质就是如下图中的三行表达式:

这里的表达式都是在进行向量计算,所以为了后面的表达方便,将其使用下面的形式表示:
ReLU(X·W^{[1]}) = A^{[1]}
\\
f_k^{[1]}(W^{[k]}_1) = a^{[1]}_k
\\\\
ReLU(A^{[1]}·W^{[2]}) = A^{[2]}
\\
f_j^{[2]}(A^{1},W^{[2]}_j) = a^{[2]}_j
\\\\
softmax(A^{2},W^{[3]})
\\
f_i^{[3]}(A^{2},W^{[3]}_i) = a^{[3]}_i
其中 i,j,k 分别对应这一层不同的神经元。
我们先来分析最下面这一个表达式:它表示的是某一个节点上要完成的计算。
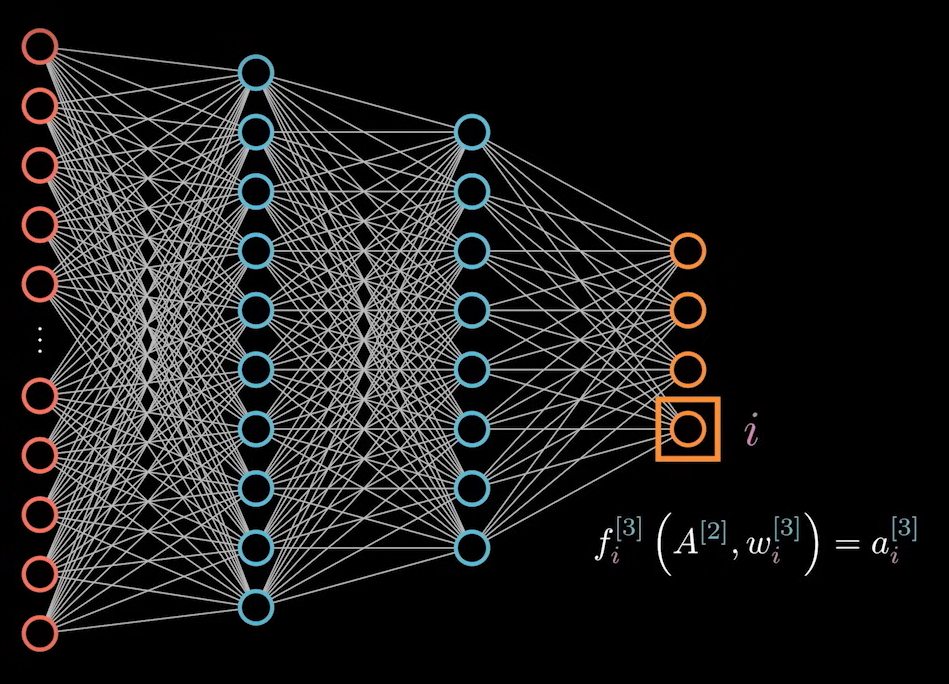
它的梯度等于:对所有变量的维度求偏导。
\nabla{f_i^{3}} =
\left[
\begin{matrix}
\frac{\partial{f^{[3]}_i}}{\partial{w^{[3]}_{i,1}}}
\\
\frac{\partial{f^{[3]}_i}}{\partial{w^{[3]}_{i,2}}}
\\ \cdots
\\
\frac{\partial{f^{[3]}_i}}{\partial{a^{[3]}_{1}}}
\\
\frac{\partial{f^{[3]}_i}}{\partial{a^{[3]}_{2}}}
\\
\cdots
\end{matrix}
\right]
这里同时也要对 A 求偏导,因为 A 也是一个当前节点的输入数据,关系如下:
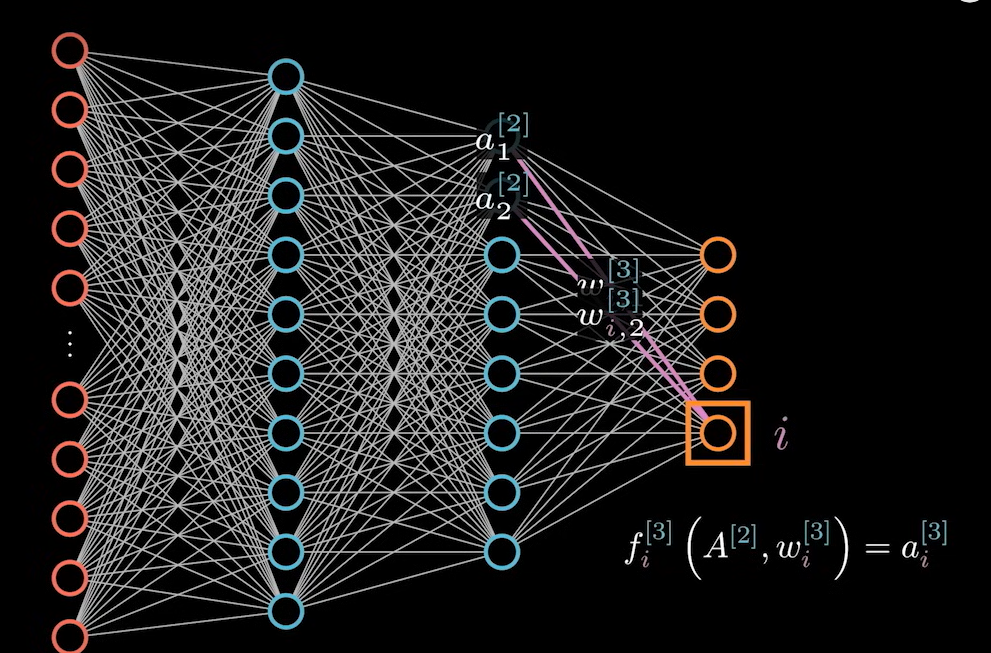
我们在考虑之前一个神经元的参数求导时,需要结合前面一层神经元的影响,即 J 层的 a 系数的偏导表达式为:
W_j^{[2]} \pm \eta^2·\frac{\partial{f_j^{[2]}}}{\partial{W_j^{[2]}}}\sum_{i=1}^4\frac{\partial{f_i^{[3]}}}{\partial{f_j^{[2]}}}
K 层的偏导系数的表达式为:
W_k^{[1]} \pm \eta^3\sum_{j=1}^7\sum_{i=1}^4\frac{\partial{f_k^{[1]}}}{\partial{W_k^{[1]}}}\frac{\partial{f_j^{[2]}}}{\partial{f_k^{[1]}}}\frac{\partial{f_i^{[3]}}}{\partial{f_j^{[2]}}}
如果反向传播的次数越多,那么学习率的次数就越高。我们知道学习率往往是小于 1 的,那么经过次方运算之后再和梯度相乘,就不会对参数做出多少调整,这也是我们经常说的梯度消失问题。
总结
到这里为止,就描述完了神经网络里的模型,算法和策略。